The Future of Areas/Triangles
How do computers draw polygons? By splitting them into adjacent triangles. Being the most basic form of polygon, they're easy to work with.
<triangle id='1'> <nd ref='101'/> <nd ref='102'/> <nd ref='103'/> (Constrained to three nodes, always) </triangle> <area id='1'> <tr ref='1'> <tr ref='2'> </area>
Advantages
Easy to get out of the DB and convert them into a OGC Polygon - just build the WKT for every triangle, compute the union of every triangle, you're done.
Consistency: Areas will always be closed, no matter what. No need to worry about inner rings or node ordering.
Disadvantages
- A bit of extra space used for storage.
| today | with triangles |
<way id="1"> <node ref="1" /> <node ref="2" /> <node ref="3" /> <node ref="4" /> <node ref="1" /> <tag k="building" v="yes" /> </way> |
<triangle id='1'> <nd ref='1'> <nd ref='2'> <nd ref='3'> </triangle> <triangle id='2'> <nd ref='1'> <nd ref='3'> <nd ref='4'> </triangle> <area id='1'> <tr ref='1'> <tr ref='2'> <tag k="building" v="yes" /> </area> |
- Added complexity for editors (either let users know about triangles and allow editing, or transparently convert them).
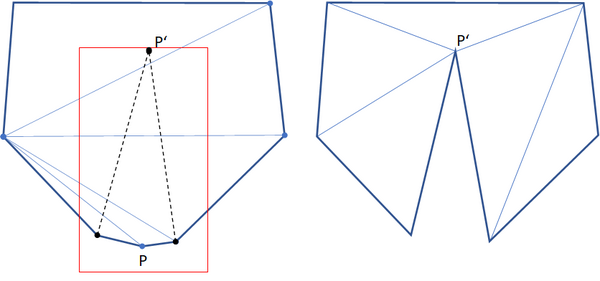
- a "local" change (within the red bounding box) might require a complete new triangulation of the polygon:, e.g. when a node is moved from position P to P':
Variations
Do not implement an "area" primitive, and handle everything with relations.
Allow tags on triangles.
Enforce a tesselation of the entire planet. That is, make sure no two triangles overlap. That may need either topological operators at the API level (split a triangle segment and remove a vertex) or extra topological checks whenever areas are included in a request (juggle triangles as needed).