User:Maxbe/Routen über Flächen

Worum geht's?

Üblicherweise kennen Routingalgorithmen zwei Dinge: Knoten (das sind Punkte) und Kanten (die Wege dazwischen). Zwischen zwei Punkten gibt es immer eine Kante, falls sich zwei Kanten einen Start- oder Endpunkt teilen, kann man dort von einer Kante auf die andere Wechseln. Dieses Gebilde aus Kanten und Knoten nennt man Routinggraph.

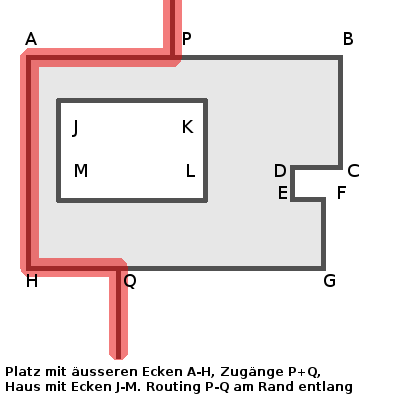
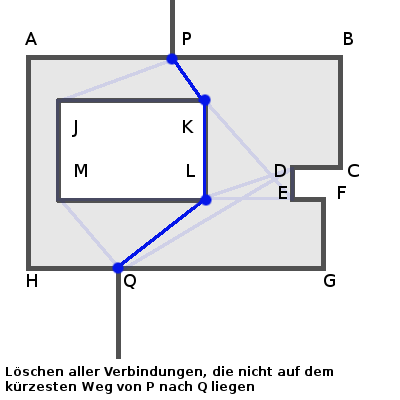
Was in diesem Modell fehlt, sind Flächen, die in OpenStreetMap z.B. als Fussgängerzonen mit (highway=pedestrian ; area=yes) eingetragen werden. Die werden von den Routern üblicherweise auch nur als Folge von Kanten in den Graphen eingetragen. Der Weg über einen solchen Platz führt dann immer am Rand entlang. Hier z.B. führt der Weg von P nach Q über A und H:

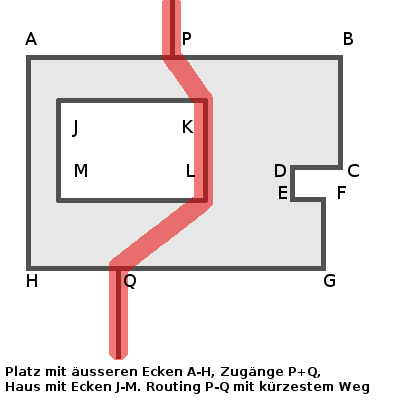
Ahilfe schafft das manuelle Mappen von zusätzlichen Wegen über den Platz. Das wird aber oft nicht gemacht und auch dort wo es gemacht wird, werden häufig nur einige der Zugänge zum Platz verbunden und andere vergessen. So entstand im Forum die Idee, automatisch virtuelle Wege in den Graphen einzufügen, die das Routen auf der kürzesten Strecke ermöglichen:

Abgrenzung: Worum geht's nicht?

Die Frage "Wie komme ich vom Platz runter, wenn ich da irgendwo drauf bin?" wird nicht gelöst. Das lässt sich nicht durch Vorarbeiten am Graphen mit bekannten Punkten lösen, sondern muss zur Laufzeit des Navigationsprogramms spontan gelöst werden. Weiter unten in diesem Text wird zwar beschrieben, dass das Verfahren so ein bisschen helfen kann, aber praxistauglich ist das nicht.

Vorbereitung der Flächen

Ausschneiden der Löcher

Fussgängerzonen sind gelegentlich Multipolygon-Relationen mit Löchern, häufiger aber ganz normale Flächen. Entgegen der Vermutung, dass man dort überall rumlaufen könnte, stehen dort jede Menge Hindernisse rum, die man erst aus der Fussgängerzone ausschneiden muss, um den betretbaren Bereich zu bekommen.

• Flächige Hindernisse (Häuser, Brunnen, Denkmäler, betretenverbotener Rasen...) sind recht einfach auszuschneiden, einfach die Flächen subtrahieren.

• Punktförmige Hindernisse (Papierkörbe, Bäume, Parkbänke, Fahrradständer, als Punkt gemappte Brunnen oder Verkaufsstände...) sind schwieriger: Da muss man zu jedem Typ von Hindernis noch eine Fläche bestimmen, die das Hindernis einnimmt. Also z.B. 1qm für einen Baum, 10qm für ein Denkmal, 60qm für eine Imbissbude.

• Linienartige Hindernisse (Mauern, Hecken, Bäche...) können als schmale Streifen mit z.B. 1 Meter Breite ausgeschnitten werden.

• Verbindungselemente sind dazu da, linienartige Hindernisse zu durchbrechen (Tore, Gatter, Furten). Die werden auch als kleine Fläche betrachtet, werden allerdings nicht aus der Fussgängerzone ausgeschnitten, sondern aus den linienartigen Hindernissen.

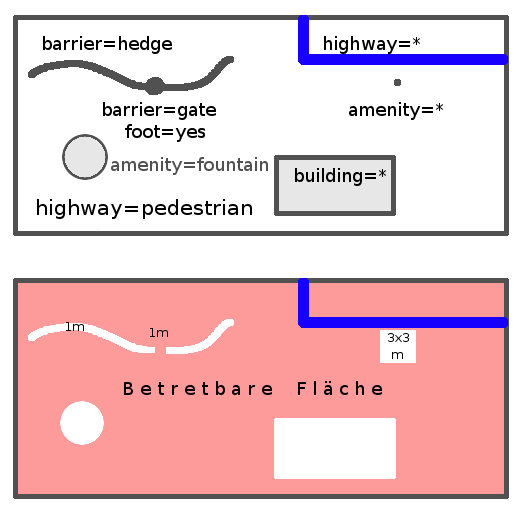
Ein Platz mit Hecke, Brunnen, amenity (z.B. Fahrradständer) und einem Haus wird z.B. so in eine "betretbare Fläche" (rot) mit weissen Löchern verwandelt. Eventuell schon über den Platz führende Wege (blau) werden ignoriert:

Die Auswahl der Hindernisse ist natürlich Geschmacksache. Klar ist, dass z.B. Mauern, Hecken, Teiche nicht begehbar sind. Ob z.B. ein Rasen oder ein Spielplatz betreten werden darf könnte durch access-Regeln beeinflusst werden, vernünftige Defaultwerte können ja trotzdem gewählt werden. Ob ein Baum oder ein Papierkorb den Rechenaufwand lohnt, hängt vom Prozessor und der Zeit ab.

Die Grösse punktförmiger Hindernisse ist ebenfalls Geschmacksache. Ein Baum wird vermutlich mit 1 Meter Freiraum gut umgangen werden können, ein Brunnen wird oft breiter sein...

In den folgenden Beispielen wird so ziemlich jede Art von Mobiliar der Plätze zumindest als 2x2 Meter grosses Hindernis betrachtet. Es hat Vorteile einfach "amenity=*" zu umrouten, weil man dann auch die Dinge sieht, an die man nicht dachte. In der Praxis wird man da sorgfältiger auswählen, jedes Hindernis vervielfacht den Rechenaufwand.

Bestimmen der wichtigen Punkte

"Wichtige Punkte" eines Platzes sind alle Punkte, die einen Zugang zu ihm vermitteln. Ausserdem können noch weitere Punkte auf dem Platz dazu erklärt werden. Z.B. könnte man einen "tourism=viewpoint" aufnehmen, oder einfach jeden Punkt eines schon vorhandenen Weges. Das hilft dann, auch Treppenabgänge auf dem Platz mit in das Flächenrouting einzubeziehen.

Bestimmen der wichtigen Ecken

Als Zwischenpunkte auf dem Weg über den Platz kommen nur die konkaven Ecken in Frage. Es hätte keinen Sinn, im Beispiel oben die Ecken B, C, F, G, H oder A aufzusuchen, weil von dort müsste man sicher wieder irgendwie zurück in die Mitte des Platzes.

In PostGis gibt es die praktische Funktion "ST_ForceRHR". Die dreht jedes (Multi-)Polygon so, dass die Grenzen der äusseren Ringe im Uhrzeigersinn den Platz umrunden, die inneren Ringe gegen den Uhrzeigersinn. Der Platz liegt also immer auf der rechten Seite der Grenzlinie (RHR=right hand rule) und die konkaven Ecken sind einfach dadurch zu bestimmen, dass man Linkskurven sucht.

Das Layer-Problem

Beim Ausschneiden der Hindernisse und dem Verbinden mit vorhandenen Wegen trifft man auf zwei Hindernisse im ZUsammenhang mit den Layer-Tags.

• Viele Flächen sind ohne ersichtlichen Grund als layer=-1 getagged. Das kann man nicht ignorieren, weil viele Fussgängerzonen sich tatsächlich gestapelt unter und über anderen Verkehrswegen befinden. Dummerweise befinden sich aber die Häuser über diesen layer=-1 -Flächen auf layer=0. Ob man diese Flächen ausschneiden darf oder nicht, ist nicht entscheidbar.

• Wege haben Layer-Angaben. Ihre Nodes aber nicht. Stösst nun ein Weg mit layer=-1 auf einen Weg mit layer=0, ist schwer zu sagen, auf welchem Layer der Verbindungspunkt liegt.

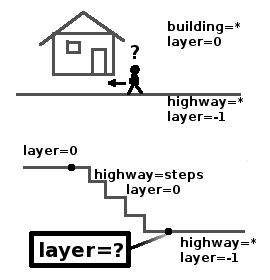
Die Lösung ist aber zum Glück ganz einfach: Man ignoriert alle unterirdischen Fussgängerzonen, es gibt oben genug zu tun. Jeder Node, der zu mindestens einem Weg gehört, der nicht auf Layer=0 liegt, wird ebenfalls ignoriert. Damit verschenkt man zwar ein paar Punkte, was besonders dann schade ist, wenn das Zugangspunkte zum Platz sind, aber man kann sicher sein, dass niemand die falsche Seite der Treppe im Bild rechts erwischt.

Eintragen der virtuellen Wege

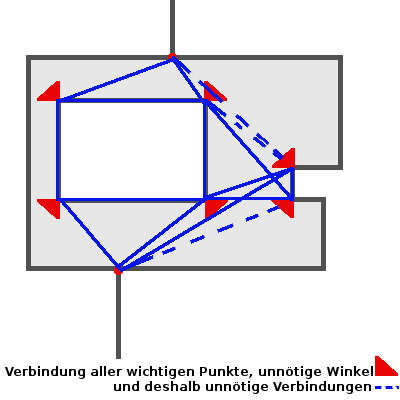
Wenn man alle Löcher hat und alle Punkte aufgelistet, zieht man einfach von jedem Punkt zu jedem anderen eine Linie. Nach einem Theorem von Netzwolf kann man dabei bei jedem Eckpunkt die Linien weglassen, die im einem so spitzen Winkel von ihm weggehen, dass die Linie zwischen den Verlängerungen der beiden Grenzlinien an dieser Ecke liegt. Im Beispiel unten sind das nicht allzu viele, die unnötigen Winkel sind auch alle nur 90 Grad. Bei Flächen mit sehr flach abgewinkelten Grenzen kann man so aber sehr viele Linien ignorieren:

Löschen der überflüssigen Linien

Diese massenhaft eingemalten Linien wirft man nun einem Routing-Algorithmus vor und lässt sich die kürzeste Verbindung von zwischen je zwei Zugangspunkten (oder auch zusätzlich den Treppen, Aussichtspunkten...) ausgeben. Die markiert man sich und löscht am Ende die Wege, die nicht markiert sind. Übrig bleibt im Beispiel nur der Weg P-K-L-Q.

Löschen der fast überflüssigen Wege

Für grosse Flächen mit komplexen Formen können so auch mal ein paar Hundert Linien entstehen, und auch nach dem Löschen der überflüssigen Wege können noch sehr viele übrig bleiben. Deshalb werden bei mir die Wege vor Beginn des Routings mit einem Zuschlag von 10% verlängert. Dann wird die erste Verbindung gesucht, und die Wege dieser Verbindung bekommen den Zuschlag wieder abgezogen. Dann wird die zweite Verbindung gesucht, Zuschlag weg, dritte Verbinden...

Auf diese Weise werden einmal gefundene Wege auch bei weiteren Verbindungssuchen bevorzugt. Auch wenn sie einen etwas weiteren Weg vermitteln. Das was übrig bleibt, sind jedenfalls Wege, die nicht mehr als 10% schlechter sind als der optimale Weg.

Die 10% sind natürlich auch Geschmacksache. Mehr als 40% sollten es aber nicht sein, sagt Pythagoras. Sonst könnte man nicht mal einen quadratischen Platz diagonal überqueren.

Zahlen

Mein Testgebiet (ca. 10E-15E 46N-49N, Stuttgart bis Linz und Trient bis Regensburg) hat 4.89 Mio Wege. Durch die 220000 virtuellen Wege wurde der Graph um 4.5% aufgeblasen. Nach dem Löschen der für die Überquerung unnötigen Wege blieben 26000 übrig, ein Zuwachs um 0.5%.

Im Stadtgebiet von München gibt es natürlich verhältnismässig mehr Fussgängerzonen. Dort wurden die vorhandenen 1.4 Mio Wege um 35000 (25%) aufgeblasen. Nach dem Löschen blieben noch 2682 übrig, ein Zuwachs um 1.9%.

Start- oder Zielpunkt auf der Fläche

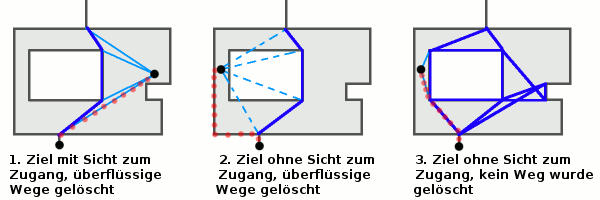
Falls der Start- oder Zielpunkt auf der Fläche liegt, könnte man ebenfalls das gasnze Verfahren durchspielen. Das muss allerdings zur Laufzeit des Navigationsprogramms passieren (und falls das Navi sich bewegt, muss das ständig passieren). Es reicht dabei nicht, nur die Verbindungen von einem Punkt zu den Zugangspunkten zu berechnen, zwischen Punkt und Zugang könnte ja ein Hindernis stehen...

Hier liegt im Bild 1 der Zugang in Sichtlinie des Zielpunktes, der Weg kann in einem Durchgang ("Berechne alle Kanten zwischen vorhandenen Wegpunkten und dem Ziel") ermittelt werden. Im Bild 2 ist das nicht möglich, keine der Kanten zum Zielpunkt (hellblau) erreicht den Zugang oder einen vorhandenen Weg (dunkelblau). Der Router würde als Notlösung über die Kante routen (rot).

Würde man auf das Löschen der "überflüssigen" (also genauer: der für die Überquerung überflüssigen) Wege verzichten und alle virtuellen Kanten stehen lassen, könnte man auch in dieser Situation den optimalen Weg ermitteln (rechtes Bild). Der Preis dafür ist ein um 25% aufgeblähter Graph in München. Die Mehrarbeit durch diese zusätzlichen Kanten fällt auch dann an, wenn eine Route nicht über Plätze führt, sondern nur in der Nähe vorbeiführt....

Beispiele

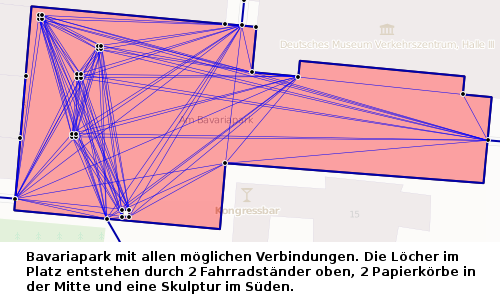
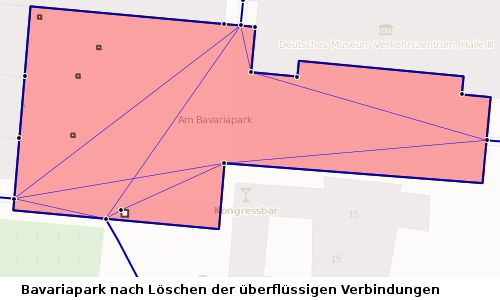
Das ist der Platz am Bavariapark in München. An allen vier Seiten führt ein Weg rauf, vier Hindernisse stehen über den Platz verteilt. Nach dem Eintragen sämtlicher Verbindungen sieht der Routinggraph so aus:

Und nach Löschen der unnötigen Wege so:

Der Extremfall in meiner Gegend ist der Platz vor dem Ludwigsburger Schloss. Dort hat ein fleissiger Mapper die Hecken sehr detailiert eingetragen, was zu sehr vielen Eckpunkten führt. Allerdings wurden ebenso detailiert schon Wege über diese Fussgängerzone angelegt. Hier wird also ziemlich lange gerechnet um ein paar Tausend virtuelle Wege zu malen, nur um anschliessend fast alle wieder zu löschen, weil sie auch nicht viel besser sind als das bereits gemappte.

Für solche Flächen empfiehlt sich eine Notbremse: Sind mehr als 100 Eckpunkte beteiligt, wird der Platz übersprungen. Das Bild oben zeigt auch nicht sämtliche virtuellen Wege, sondern nur den Zustand nach der Hälfte der Berechnung, damit nicht alles blau wird.

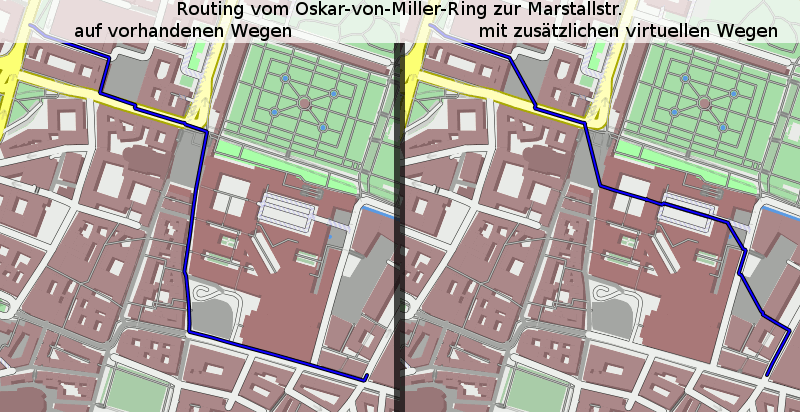
Als letztes Beispiel noch der Vergleich zwischen Randrouting und Flächenrouting. Der Weg vom Wittelsbacherplatz über den Platz vor der Feldherrnhalle durch die Residenz zum Marstallplatz (hier als Track auf der Karte). Ohne virtuelle Wege würde der Router eher den Strassen folgen und die Plätze vermeiden.

weitere Quellen

Eine Gruppe aus Graz hat sich der Fußgänger und der Flächen angenommen und ein Paper bei gis.Open Paper veröffentlicht: Optimierte Wegefindung für Fußgänger basierend auf vorhandenen OpenStreetMap-Daten

openplans.org kann ebenfalls über Flächen routen und hat in seinem Blog was dazu geschrieben: b-roll: David solves the plaza problem, with help from de Berg and Matt Conway

An der RWTH hatten ein paar Leute die Idee, die Flächen mit einem Netz aus Wegen zu überziehen und routen über Flächen auf diesem "SpiderWebGraph".

Siehe auch diese Forschungsarbeit von der HSR: https://eprints.hsr.ch/625/ und https://github.com/PlazaRoute/plazaroute .