Roof 3D modeling
The 3D modeling techniques described in this page are based on S3DB definition and Kendzi 3D PlugIn for JOSM.
Roof with one slope
This very common but for the most users complicated roof needs in addition to roof:shape=skillion still the rotation definition - means the from top to down direction of fall of water on the roof.
This angle is described as roof:direction=<value in degrees>.
An example shows how to easily determine this angle and what could be done wrong:
An existing building=yes with roof:shape=hipped shape:
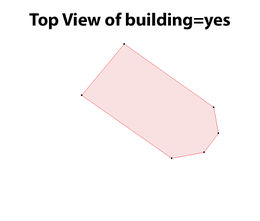
The so called skeleton algorithm generates following 2d result:
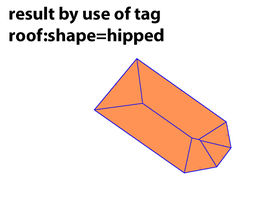
And as 3D model we would get this:
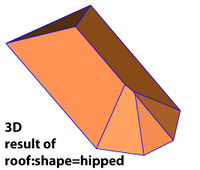
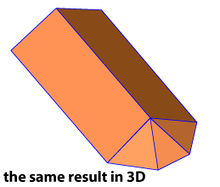
Our wishful result should look different:

This can be realized only by use of tag roof:direction=* for each surface:
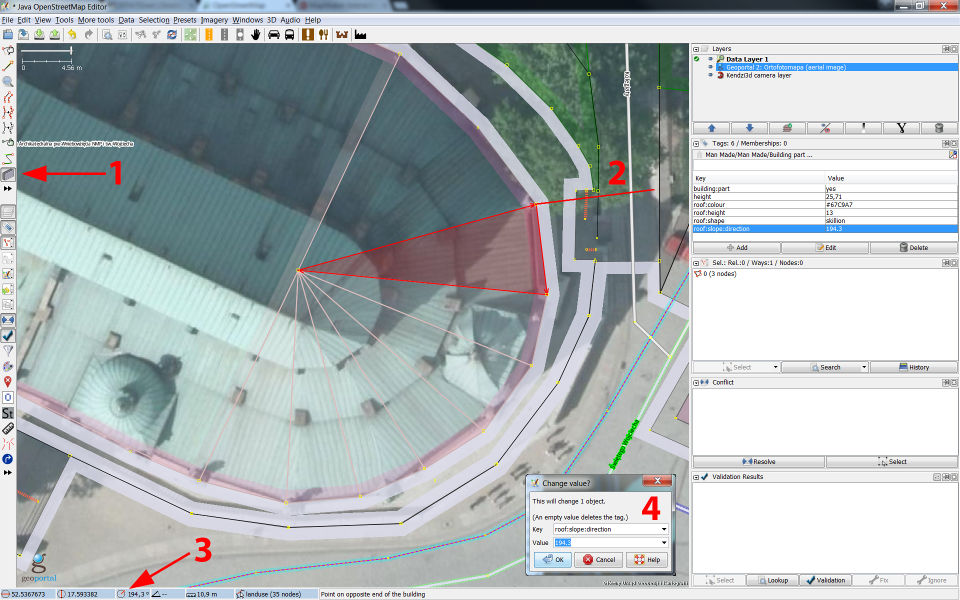
Measurement of roof:direction=*
This method need in JOSM Plug In: BuildingTools
Activate the wishful roof polygon and add the attributes: roof:shape=skillion+ roof:direction=*
- Click on the BuildingTools symbol
- Draw the building, starting from the lowest part (corner) of the roof to the highest point (peak) of the roof.
- Complete the polygon by drawing back to the starting point.
- The
roof:direction=*angle can be found at the bottom of JOSM as marked by note 3 in the figure below.- For square or rectangular roofs, you can note the angle as you draw your line down the roof.
- For non-square roof segments, as in the figure below, drawing a temporary line from the highest part of the roof to the lowest will provide you with the angle needed.
- Enter this value into the
roof:direction=*tag and remove the temporary line, if one was created.
Enjoy the modelling!
Sphere modelling
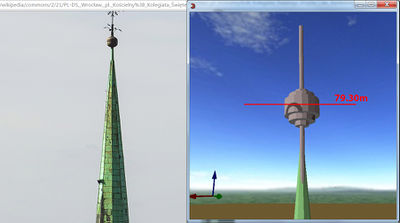
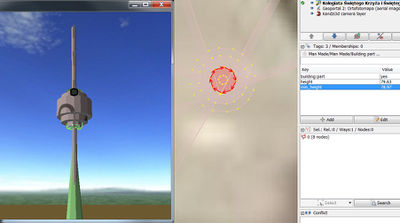
I know from Wikipedia, the height=* of the tower in "my" building is 80m
I assume, the middle of the tower is 79.30m.
Because there is no sphere in the specification, I construct a sheet model:
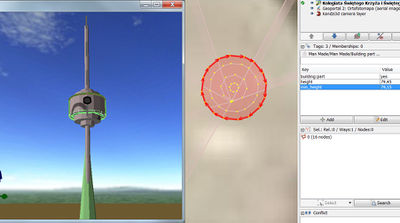
400px this sketch help me to avoid wrong height values:
Sheet no. 1.:
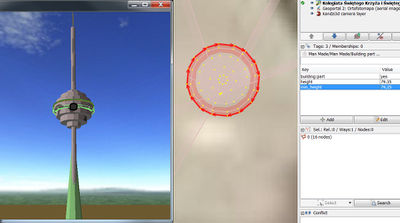
Sheet no. 2.:
Sheet no. 3.:
I decide, this looks not good enough and add one sheet more:
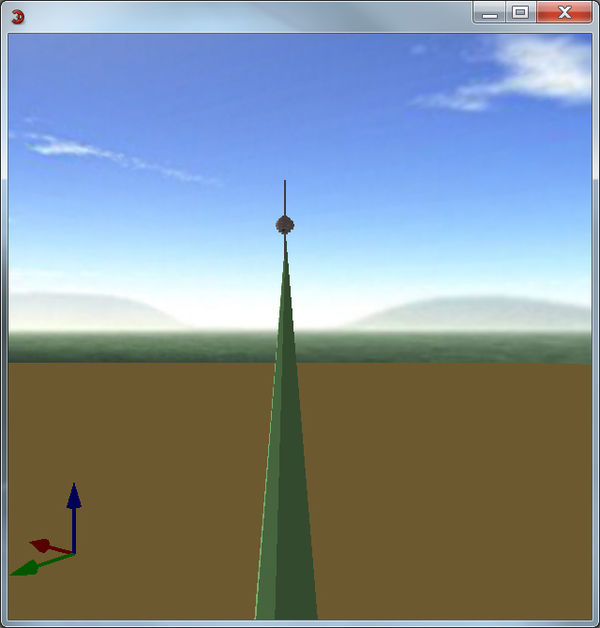
The result now:
Complex shapes
The approach is easy to understand: Try to divide complicated geometries in simple elements. Similar to cone modeling. The difference to, let´s say Lego elements, is the possibility of spatial overlapping, fusion of elements.
results in: