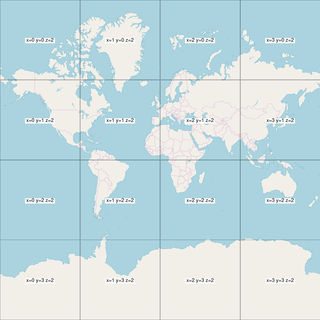
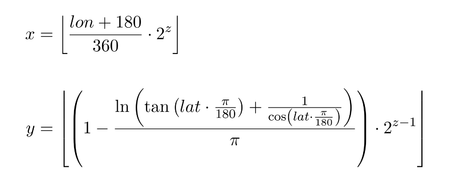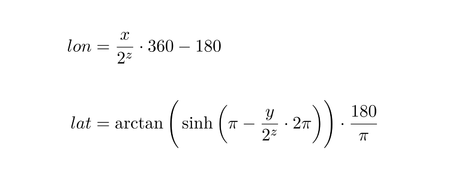Ko:Slippy map tilenames

From OpenStreetMap Wiki
Jump to navigation Jump to search
Slippy map tilenames - Other languages
Tile numbering for zoom=2

이 문서는 미끄러운 지도 애플리케이션의 파일 명명 규칙을 설명합니다.

  • 타일은 256 × 256 픽셀 PNG 파일입니다.
  • 각 확대 레벨은 디렉터리이고, 각 열은 하위 디렉터리이며, 그 열의 각 타일은 파일입니다.
  • 파일 이름(또는 URL) 형식은 /zoom/x/y.png입니다.

미끄러운 지도는 이러한 형식을 따르는 URL에서 타일을 제공받기를 기대하기 때문에 모든 타일 서버 URL은 매우 유사하게 보입니다.


타일 서버

two merging arrows

이 페이지나 섹션은 TMS과 병합하는것이 제안되었습니다. (토의하기)

URL의 첫 번째 부분은 타일 서버를 지정합니다. 타일 좌표는 일반적으로 /zoom/x/y.png 형식의 꼬리로 지정됩니다. 일부 타일 서버는 특정 스타일시트를 지정하기 위해 디렉터리(e.g. "/cycle/")를 사용할 수 있습니다. (역사적으로 여러 서브도메인이 제공되어 각 호스트에 대한 동시에 열릴 수 있는 HTTP 연결 수의 브라우저 제한을 회피했지만, 현대 브라우저에서는 덜 중요합니다 - 예: a.tile, b.tile, c.tile).

다음은 몇 가지 예입니다:

이름 URL 템플릿 확대 레벨
OSM '표준' 스타일 https://tile.openstreetmap.org/zoom/x/y.png 0-19
OpenCycleMap http://[abc].tile.thunderforest.com/cycle/zoom/x/y.png 0-22
Thunderforest Transport http://[abc].tile.thunderforest.com/transport/zoom/x/y.png 0-22
MapTiles API Standard https://maptiles.p.rapidapi.com/local/osm/v1/zoom/x/y.png?rapidapi-key=YOUR-KEY 전 세계적으로 0-19
MapTiles API English https://maptiles.p.rapidapi.com/en/map/v1/zoom/x/y.png?rapidapi-key=YOUR-KEY 전 세계적으로 0-19 (영어 타일셋 제공)

다양한 '써드파티' 출처로부터 추가 타일셋을 사용할 수 있습니다.

확대 레벨

확대 파라미터는 0(축소)에서 18(확대) 사이의 정수입니다. 18이 일반적으로 최대이지만, 일부 타일 서버는 그 이상을 지원할 수 있습니다.

확대 레벨 타일 커버 범위 타일 수 타일 크기(*) (도 단위)
0 1개의 타일이 전 세계를 덮음 1개 360° x 170.1022°
1 2 × 2 타일 4개 180° x 85.0511°
2 4 × 4 타일 16개 90° x [변수]
n 2n × 2n 타일 22n개 360/2n° x [변수]
12 4096 x 4096 타일 1677만 7216개 0.0879° x [변수]
16 232 ≈ 42억 9500만개
17 172억개
18 687억개
19 Mapnik 레이어의 최대 확대 2749억 개의 타일

(*) 모든 타일의 너비(경도)는 일정하지만, 같은 확대 수준에서 높이(위도)는 일정하지 않습니다. 일반적으로 같은 행에 속한 타일은 동일한 높이(도 단위)를 가지지만, 적도에서 극지방으로 이동할수록 높이는 줄어듭니다.

자세한 내용은 확대 레벨을 참조하세요.

타일 이름의 유도

다음은 잘 알려진 웹 메르카토르 투영법과 동일합니다.

  • 좌표를 구형 메르카토르 투영법으로 재투영합니다 (EPSG:4326에서 EPSG:3857로):
    • x = lon
    • y = arsinh(tan(lat)) = log[tan(lat) + sec(lat)]
    (lat와 lon은 라디안 단위입니다)
  • x와 y의 범위를 0 – 1로 변환하고 원점을 왼쪽 상단 모서리로 이동합니다:
    • x = [1 + (x / π)] / 2
    • y = [1 − (y / π)] / 2
  • 확대를 사용하여 지도 전체의 타일 수, n를 계산합니다, 2zoom
  • x와 y에 n을 곱합니다. 결과를 내림하여 tilex와 tiley를 구합니다.

구현

의사 코드

의사 코드를 좋아하는 사람들을 위해 몇 가지 힌트를 제공합니다: 

sec = 1/cos
arsinh(x) = log(x + (x^2 + 1)^0.5)
sec^2(x) = tan^2(x) + 1
→ arsinh(tan(x)) = log(tan(x) + sec(x))

"log"는 상용로그(log10)가 아닌 자연 로그(ln 또는 loge)를 의미합니다. 일부 계산기에서 사용되는 상용로그와 혼동하지 마세요.

경도/위도를 타일 번호로 변환 

n = 2 ^ zoom
xtile = n * ((lon_deg + 180) / 360)
ytile = n * (1 - (log(tan(lat_rad) + sec(lat_rad)) / π)) / 2

타일 번호를 경도/위도로 변환 

n = 2 ^ zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = arctan(sinh(π * (1 - 2 * ytile / n)))
lat_deg = lat_rad * 180.0 / π

이 코드는 타일의 왼쪽 상단 (북서쪽) 점의 좌표를 반환합니다.

수학

수학 기호를 사용한 동일한 내용 (위도와 경도는 도 단위):

Latlon to tile.pngTile to latlon.png

예: GPS 좌표를 웹 메르카토르 타일의 픽셀 위치로 변환

관심 있는 좌표를 선택합니다.

이 예는 시부야 스크램블 교차로 근처의 하치코 동상이 어느 타일에 속해 있는지 (그리고 타일 내에서 어떤 픽셀 좌표에 위치하는지) 찾는 방법을 보여줍니다:

https://www.openstreetmap.org/node/597685675

변수 공식 예시 (하치코 동상)
lonEPSG:4326 OpenStreetMap의 노드에 기록된 익숙한 "GPS"-스타일의 경도. 양수는 동쪽이고, 음수는 서쪽입니다. +139.7006793°
latEPSG:4326 OpenStreetMap의 노드에 기록된 익숙한 "GPS"-스타일의 위도. 양수는 북쪽이고, 음수는 남쪽입니다. +35.6590699°
좌표를 웹 메르카토르 투영법으로 변환합니다. (https://epsg.io/3857)
xEPSG:3857 lonEPSG:4326이 값은 (-180°, 180°) 범위에 속하게 됩니다. 139.7006793°
yEPSG:3857 ln(tan(latEPSG:4326) + 1 / cos(latEPSG:4326))또는 arsinh(tan(latEPSG:4326))

이 값은 위도 85.0511 °S와 85.0511 °N 사이에서 (-π, π) 범위에 속하게 됩니다. 참고로, 숫자 85.0511은 arctan(sinh(π))의 결과입니다. 이 범위를 사용하면 전체 지도가 (매우 큰)정사각형이 됩니다.

0.66693624687
투영된 점을 단위 정사각형으로 변환합니다.
x 0.5 + xEPSG:3857 / 360°

이 값은 (0, 1) 범위에 속하게 됩니다. x=0은 지도에서 왼쪽 가장자리 (180° 서쪽)입니다. x=1은 지도에서 오른쪽 가장자리 (180° 동쪽)입니다. x=0.5는 중앙, 즉 본초 자오선입니다.

0.8880574425
y 0.5 − yEPSG:3857 / (2π)

이 값은 (0, 1) 범위에 속하게 됩니다. y=0은 지도에서 상단 (북쪽 가장자리)으로 85.0511 °N에 위치합니다. y=1은 지도에서 하단 (남쪽 가장자리)으로 85.0511 °S에 위치합니다. y=0.5는 중앙, 즉 적도입니다.

0.3938537996
확대 레벨과 개별 타일의 크기를 결정합니다.
확대 확대 레벨이 0일 때, 전체 지구는 단일 타일로 표시됩니다.

확대 레벨이 18일 때, 개별 도시 블록의 세부 사항이 보입니다.

18
투영된 점을 타일 공간으로 변환합니다.
N 2zoom

이는 지도 한쪽 가장자리에서 다른 가장자리까지의 가로 또는 세로 타일 수입니다.

262144
xtile N * x

xtile의 정수 부분은 해당 타일의 "x" 값을 나타냅니다. xtile의 소수 부분은 그 타일 내에서 좌표의 내부 수평 위치를 나타냅니다.

첫 번째 타일은 xtile=0이며, 왼쪽 가장자리는 180° W에 위치합니다. 마지막 타일은 xtile=2zoom−1이며, 오른쪽 가장자리는 180° E에 위치합니다.

232798.930207

tile x = 232798

fractional x = 93.02%

ytile N * y

ytile의 정수 부분은 해당 타일의 "y" 값을 나타냅니다. ytile의 소수 부분은 그 타일 내에서 좌표의 내부 수직 위치를 나타냅니다.

첫 번째 타일은 ytile=0이며, 상단 가장자리는 85.0511 °N에 위치합니다. 마지막 타일은 ytile=2zoom−1이며, 하단 가장자리는 85.0511 °S에 위치합니다.

103246.410442

tile y = 103246

fractional y = 41.04%

URL /(zoom)/(xtile)/(ytile).png대부분의 타일 서버는 위와 유사한 경로를 사용합니다.

예를 들어, 위의 계산에 따르면 하치코는 다음 위치에 있습니다: 

https://tile.openstreetmap.org/18/232798/103246.png
 103246.png
크기 관례적으로 "표준 해상도" 타일의 경우 256 픽셀입니다.

"고해상도" 또는 "레티나" 타일의 경우 일반적으로 512 픽셀입니다.

xpixel fract(xtile) * dimension

이는 0에서 크기 사이의 숫자로, 타일 내에서 이 좌표의 x 오프셋입니다.

238.1 px
ypixel fract(xtile) * dimension

이는 0에서 크기 사이의 숫자로, 타일 내에서 이 좌표의 y 오프셋입니다.

105.1 px

일반적인 프로그래밍 언어

Python

Lon./lat. to tile numbers 

import math
def deg2num(lat_deg, lon_deg, zoom):
  lat_rad = math.radians(lat_deg)
  n = 1 << zoom
  xtile = int((lon_deg + 180.0) / 360.0 * n)
  ytile = int((1.0 - math.asinh(math.tan(lat_rad)) / math.pi) / 2.0 * n)
  return xtile, ytile

Tile numbers to lon./lat. 

import math
def num2deg(xtile, ytile, zoom):
  n = 1 << zoom
  lon_deg = xtile / n * 360.0 - 180.0
  lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * ytile / n)))
  lat_deg = math.degrees(lat_rad)
  return lat_deg, lon_deg

This returns the NW-corner of the square. Use the function with xtile+1 and/or ytile+1 to get the other corners. With xtile+0.5 & ytile+0.5 it will return the center of the tile.

See also tilenames.py and the 'mercantile' library

Ruby

Lon./lat. to tile numbers 

def get_tile_number(lat_deg, lng_deg, zoom)
  lat_rad = lat_deg/180 * Math::PI
  n = 2.0 ** zoom
  x = ((lng_deg + 180.0) / 360.0 * n).to_i
  y = ((1.0 - Math::log(Math::tan(lat_rad) + (1 / Math::cos(lat_rad))) / Math::PI) / 2.0 * n).to_i
  
  {:x => x, :y =>y}
end

Tile numbers to lon./lat. 

def get_lat_lng_for_number(xtile, ytile, zoom)
  n = 2.0 ** zoom
  lon_deg = xtile / n * 360.0 - 180.0
  lat_rad = Math::atan(Math::sinh(Math::PI * (1 - 2 * ytile / n)))
  lat_deg = 180.0 * (lat_rad / Math::PI)
  {:lat_deg => lat_deg, :lng_deg => lon_deg}
end

Same as the Python implementation above, this returns the NW-corner of the square. Use the function with xtile+1 and/or ytile+1 to get the other corners. With xtile+0.5 & ytile+0.5 it will return the center of the tile.

Perl

Lon./lat. to tile numbers 

use Math::Trig;
sub getTileNumber {
  my ($lat,$lon,$zoom) = @_;
  my $xtile = int( ($lon+180)/360 * 2**$zoom ) ;
  my $ytile = int( (1 - log(tan(deg2rad($lat)) + sec(deg2rad($lat)))/pi)/2 * 2**$zoom ) ;
  return ($xtile, $ytile);
}

Tile numbers to lon./lat. 

use Math::Trig;
sub Project {
  my ($X,$Y, $Zoom) = @_;
  my $Unit = 1 / (2 ** $Zoom);
  my $relY1 = $Y * $Unit;
  my $relY2 = $relY1 + $Unit;

  # note: $LimitY = ProjectF(degrees(atan(sinh(pi)))) = log(sinh(pi)+cosh(pi)) = pi
  # note: degrees(atan(sinh(pi))) = 85.051128..
  #my $LimitY = ProjectF(85.0511);

  # so stay simple and more accurate
  my $LimitY = pi;
  my $RangeY = 2 * $LimitY;
  $relY1 = $LimitY - $RangeY * $relY1;
  $relY2 = $LimitY - $RangeY * $relY2;
  my $Lat1 = ProjectMercToLat($relY1);
  my $Lat2 = ProjectMercToLat($relY2);
  $Unit = 360 / (2 ** $Zoom);
  my $Long1 = -180 + $X * $Unit;
  return ($Lat2, $Long1, $Lat1, $Long1 + $Unit); # S,W,N,E
}
sub ProjectMercToLat($){
  my $MercY = shift;
  return rad2deg(atan(sinh($MercY)));
}
sub ProjectF
{
  my $Lat = shift;
  $Lat = deg2rad($Lat);
  my $Y = log(tan($Lat) + sec($Lat));
  return $Y;
}

Lon./lat. to bbox 

use Math::Trig;

sub getTileNumber {
    my ($lat,$lon,$zoom) = @_;
    my $xtile = int( ($lon+180)/360 * 2**$zoom ) ;
    my $ytile = int( (1 - log(tan(deg2rad($lat)) + sec(deg2rad($lat)))/pi)/2 * 2**$zoom ) ;
    return ($xtile, $ytile);
}

sub getLonLat {
	my ($xtile, $ytile, $zoom) = @_;
	my $n = 2 ** $zoom;
	my $lon_deg = $xtile / $n * 360.0 - 180.0;
	my $lat_deg = rad2deg(atan(sinh(pi * (1 - 2 * $ytile / $n))));
	return ($lon_deg, $lat_deg);
}

# convert from permalink OSM format like:
# https://www.openstreetmap.org/?lat=43.731049999999996&lon=15.79375&zoom=13&layers=M
# to OSM "Export" iframe embedded bbox format like:
# https://www.openstreetmap.org/export/embed.html?bbox=15.7444,43.708,15.8431,43.7541&layer=mapnik

sub LonLat_to_bbox {
	my ($lat, $lon, $zoom) = @_;

	my $width = 425; my $height = 350;	# note: must modify this to match your embed map width/height in pixels
	my $tile_size = 256;

	my ($xtile, $ytile) = getTileNumber ($lat, $lon, $zoom);

	my $xtile_s = ($xtile * $tile_size - $width/2) / $tile_size;
	my $ytile_s = ($ytile * $tile_size - $height/2) / $tile_size;
	my $xtile_e = ($xtile * $tile_size + $width/2) / $tile_size;
	my $ytile_e = ($ytile * $tile_size + $height/2) / $tile_size;

	my ($lon_s, $lat_s) = getLonLat($xtile_s, $ytile_s, $zoom);
	my ($lon_e, $lat_e) = getLonLat($xtile_e, $ytile_e, $zoom);

	my $bbox = "$lon_s,$lat_s,$lon_e,$lat_e";
	return $bbox;
}
PHP

Lon./lat. to tile numbers 

$xtile = floor((($lon + 180) / 360) * pow(2, $zoom));
$ytile = floor((1 - log(tan(deg2rad($lat)) + 1 / cos(deg2rad($lat))) / pi()) /2 * pow(2, $zoom));

Tile numbers to lon./lat. 

$n = pow(2, $zoom);
$lon_deg = $xtile / $n * 360.0 - 180.0;
$lat_deg = rad2deg(atan(sinh(pi() * (1 - 2 * $ytile / $n))));
ColdFusion

Lon./lat. to tile numbers

CFScript syntax: 

<cfscript>
    function longitude2tile(longitude, zoom) {
	    return floor((longitude + 180) / 360 * (2 ^ zoom));
	    }

    function latitude2tile(latitude, zoom) {
	    return floor((1 - log(tan(latitude * pi() / 180) + 1 / cos(latitude * pi() / 180)) / pi()) / 2 * (2 ^ zoom));
	    }

    xtile = longitude2tile(longitude, zoom);
    ytile = latitude2tile(latitude, zoom);
</cfscript>

CFML syntax: 

<cffunction name="longitude2tile" output="no" returntype="numeric">
	<cfargument name="longitude" type="numeric" required="yes" />
	<cfargument name="zoom" type="numeric" required="yes" />
	<cfreturn floor((arguments.longitude + 180) / 360 * (2 ^ arguments.zoom)) />
</cffunction>

<cffunction name="latitude2tile" output="no" returntype="numeric">
	<cfargument name="latitude" type="numeric" required="yes" />
	<cfargument name="zoom" type="numeric" required="yes" />
	<cfreturn floor((1 - log(tan(arguments.latitude * pi() / 180) + 1 / cos(arguments.latitude * pi() / 180)) / pi()) / 2 * (2 ^ arguments.zoom)) />
</cffunction>

<cfset xtile = longitude2tile(longitude, zoom) />
<cfset ytile = latitude2tile(latitude, zoom) />

Tile numbers to lon./lat.

CFScript syntax: 

<cfscript>
    function tile2longitude(xtile, zoom) {
	    return (xtile / (2 ^ zoom) * 360 - 180);
	    }

    function tile2latitude(ytile, zoom) {
	    var n = pi() - 2 * pi() * ytile / (2 ^ zoom);
	    return (180 / pi() * atn(0.5 * (exp(n) - exp(-n))));
	    }

    longitude = tile2longitude(xtile, zoom);
    latitude = tile2latitude(ytile, zoom);
</cfscript>

CFML syntax: 

<cffunction name="tile2longitude" output="no" returntype="numeric">
	<cfargument name="xtile" type="numeric" required="yes" />
	<cfargument name="zoom" type="numeric" required="yes" />
	<cfreturn (arguments.xtile / (2 ^ arguments.zoom) * 360 - 180) />
</cffunction>

<cffunction name="tile2latitude" output="no" returntype="numeric">
	<cfargument name="ytile" type="numeric" required="yes" />
	<cfargument name="zoom" type="numeric" required="yes" />
	<cfset var n = pi() - 2 * pi() * arguments.ytile / (2 ^ arguments.zoom) />
	<cfreturn (180 / pi() * atn(0.5 * (exp(n) - exp(-n)))) />
</cffunction>

<cfset longitude = tile2longitude(xtile, zoom) />
<cfset latitude = tile2latitude(ytile, zoom) />
ECMAScript (JavaScript/ActionScript, etc.)
 function lon2tile(lon,zoom) { return (Math.floor((lon+180)/360*Math.pow(2,zoom))); }
 function lat2tile(lat,zoom)  { return (Math.floor((1-Math.log(Math.tan(lat*Math.PI/180) + 1/Math.cos(lat*Math.PI/180))/Math.PI)/2 *Math.pow(2,zoom))); }

Inverse process: 

 function tile2long(x,z) {
  return (x/Math.pow(2,z)*360-180);
 }
 function tile2lat(y,z) {
  var n=Math.PI-2*Math.PI*y/Math.pow(2,z);
  return (180/Math.PI*Math.atan(0.5*(Math.exp(n)-Math.exp(-n))));
 }

Example for calculating number of tiles within given extent and zoom-level: 

var zoom        = 9;
var top_tile    = lat2tile(north_edge, zoom); // eg.lat2tile(34.422, 9);
var left_tile   = lon2tile(west_edge, zoom);
var bottom_tile = lat2tile(south_edge, zoom);
var right_tile  = lon2tile(east_edge, zoom);
var width       = Math.abs(left_tile - right_tile) + 1;
var height      = Math.abs(top_tile - bottom_tile) + 1;

// total tiles
var total_tiles = width * height; // -> eg. 377

Example: Tilesname WebCalc V1.0


Lon./lat. to bbox 

const EARTH_CIR_METERS = 40075016.686;
const TILE_SIZE = 256
const degreesPerMeter = 360 / EARTH_CIR_METERS;
const LIMIT_Y = toDegrees(Math.atan(Math.sinh(Math.PI))) // around 85.0511...

function toRadians(degrees) {
  return degrees * Math.PI / 180;
}
function toDegrees(radians) {
  return (radians / Math.PI) * 180
}

function tile2long(x,z) {
  return (x/Math.pow(2,z)*360-180);
}

function lonOnTile(lon, zoom) {
  return ((lon + 180) / 360) * Math.pow(2, zoom)
}
function tile2lat(y,z) {
  const n=Math.PI-2*Math.PI*y/Math.pow(2,z);
  return (180/Math.PI*Math.atan(0.5*(Math.exp(n)-Math.exp(-n))));
}

function latOnTile(lat, zoom) {
  return (
    ((1 -
      Math.log(
        Math.tan((lat * Math.PI) / 180) + 1 / Math.cos((lat * Math.PI) / 180)
      ) /
        Math.PI) /
      2) *
    Math.pow(2, zoom)
  )
}
 

function latLngToBounds(lat, lng, zoom, width, height){ // width and height must correspond to the iframe width/height
  const metersPerPixelEW = EARTH_CIR_METERS / Math.pow(2, zoom + 8);

  const shiftMetersEW = width/2 * metersPerPixelEW;

  const shiftDegreesEW = shiftMetersEW * degreesPerMeter;
  
  const southTile = (TILE_SIZE * latOnTile(lat, zoom) + height/2) / TILE_SIZE
  const northTile = (TILE_SIZE * latOnTile(lat, zoom) - height/2) / TILE_SIZE


  return {
    south: Math.max(tile2lat(southTile, zoom), -LIMIT_Y),
    west: lng-shiftDegreesEW,
    north: Math.min(tile2lat(northTile, zoom), LIMIT_Y),
    east: lng+shiftDegreesEW
  }
}

// Usage Example: create the src attribute for Open Street Map:
const latitude = 47
const longitude = 12
const zoom = 16
const width = 450
const height = 350

const bb = latLngToBounds(latitude,longitude,zoom,width,height);

const src = [
  "https://www.openstreetmap.org/export/embed.html?bbox=",
  bb.west,
  ",",
  bb.south,
  ",",
  bb.east,
  ",",
  bb.north,
  "&layer=mapnik&marker=",
  latitude,
  ",",
  longitude,
].join('');
C/C++
int long2tilex(double lon, int z) 
{ 
	return (int)(floor((lon + 180.0) / 360.0 * (1 << z))); 
}

int lat2tiley(double lat, int z)
{ 
    double latrad = lat * M_PI/180.0;
	return (int)(floor((1.0 - asinh(tan(latrad)) / M_PI) / 2.0 * (1 << z))); 
}

double tilex2long(int x, int z) 
{
	return x / (double)(1 << z) * 360.0 - 180;
}

double tiley2lat(int y, int z) 
{
	double n = M_PI - 2.0 * M_PI * y / (double)(1 << z);
	return 180.0 / M_PI * atan(0.5 * (exp(n) - exp(-n)));
}
C#
int long2tilex(double lon, int z)
{
    return (int)(Math.Floor((lon + 180.0) / 360.0 * (1 << z)));
}

int lat2tiley(double lat, int z)
{
    var latRad = lat / 180 * Math.PI;
    return (int)Math.Floor((1 - Math.Log(Math.Tan(latRad) + 1 / Math.Cos(latRad)) / Math.PI) / 2 * (1 << z));
}

double tilex2long(int x, int z)
{
    return x / (double)(1 << z) * 360.0 - 180;
}

double tiley2lat(int y, int z)
{
    double n = Math.PI - 2.0 * Math.PI * y / (double)(1 << z);
    return 180.0 / Math.PI * Math.Atan(0.5 * (Math.Exp(n) - Math.Exp(-n)));
}
Go


Example(Deg2num had changed below.) : [1] Doc : [2] 

import (
	"math"
)

type Tile struct {
	Z    int
	X    int
	Y    int
	Lat  float64
	Long float64
}

type Conversion interface {
	deg2num(t *Tile) (x int, y int)
	num2deg(t *Tile) (lat float64, long float64)
}

func (*Tile) Deg2num(t *Tile) (x int, y int) {
	n := math.Exp2(float64(z))
	x = int(math.Floor((lon + 180.0) / 360.0 * n))
	if float64(x) >= n {
		x = int(n - 1)
	}
	y = int(math.Floor((1.0 - math.Log(math.Tan(lat*math.Pi/180.0)+1.0/math.Cos(lat*math.Pi/180.0))/math.Pi) / 2.0 * n))
	return
}

func (*Tile) Num2deg(t *Tile) (lat float64, long float64) {
	n := math.Pi - 2.0*math.Pi*float64(t.Y)/math.Exp2(float64(t.Z))
	lat = 180.0 / math.Pi * math.Atan(0.5*(math.Exp(n)-math.Exp(-n)))
	long = float64(t.X)/math.Exp2(float64(t.Z))*360.0 - 180.0
	return lat, long
}
Java
 public class slippytest {
 public static void main(String[] args) {
   int zoom = 10;
   double lat = 47.968056d;
   double lon = 7.909167d;
   System.out.println("https://tile.openstreetmap.org/" + getTileNumber(lat, lon, zoom) + ".png");
 }
 public static String getTileNumber(final double lat, final double lon, final int zoom) {
   int xtile = (int)Math.floor( (lon + 180) / 360 * (1<<zoom) ) ;
   int ytile = (int)Math.floor( (1 - Math.log(Math.tan(Math.toRadians(lat)) + 1 / Math.cos(Math.toRadians(lat))) / Math.PI) / 2 * (1<<zoom) ) ;
    if (xtile < 0)
     xtile=0;
    if (xtile >= (1<<zoom))
     xtile=((1<<zoom)-1);
    if (ytile < 0)
     ytile=0;
    if (ytile >= (1<<zoom))
     ytile=((1<<zoom)-1);
    return("" + zoom + "/" + xtile + "/" + ytile);
   }
 }

Tile bounding box 

  class BoundingBox {
    double north;
    double south;
    double east;
    double west;   
  }
  BoundingBox tile2boundingBox(final int x, final int y, final int zoom) {
    BoundingBox bb = new BoundingBox();
    bb.north = tile2lat(y, zoom);
    bb.south = tile2lat(y + 1, zoom);
    bb.west = tile2lon(x, zoom);
    bb.east = tile2lon(x + 1, zoom);
    return bb;
  }

  static double tile2lon(int x, int z) {
     return x / Math.pow(2.0, z) * 360.0 - 180;
  }

  static double tile2lat(int y, int z) {
    double n = Math.PI - (2.0 * Math.PI * y) / Math.pow(2.0, z);
    return Math.toDegrees(Math.atan(Math.sinh(n)));
  }
Kotlin
import kotlin.math.*

fun getXYTile(lat : Double, lon: Double, zoom : Int) : Pair<Int, Int> {
        val latRad = Math.toRadians(lat)
        var xtile = floor( (lon + 180) / 360 * (1 shl zoom) ).toInt()
        var ytile = floor( (1.0 - asinh(tan(latRad)) / PI) / 2 * (1 shl zoom) ).toInt()

        if (xtile < 0) {
            xtile = 0
        }
        if (xtile >= (1 shl zoom)) {
            xtile= (1 shl zoom) - 1
        }
        if (ytile < 0) {
            ytile = 0
        }
        if (ytile >= (1 shl zoom)) {
            ytile = (1 shl zoom) - 1
        }

        return Pair(xtile, ytile)
}

VB.Net
Private Function CalcTileXY(ByVal lat As Single, ByVal lon As Single, ByVal zoom As Long) As Point
   CalcTileXY.X  = CLng(Math.Floor((lon + 180) / 360 * 2 ^ zoom))
   CalcTileXY.Y = CLng(Math.Floor((1 - Math.Log(Math.Tan(lat * Math.PI / 180) + 1 / Math.Cos(lat * Math.PI / 180)) / Math.PI) / 2 * 2 ^ zoom))
End Function
C#
		
public PointF WorldToTilePos(double lon, double lat, int zoom)
{
	PointF p = new Point();
	p.X = (float)((lon + 180.0) / 360.0 * (1 << zoom));
	p.Y = (float)((1.0 - Math.Log(Math.Tan(lat * Math.PI / 180.0) + 
		1.0 / Math.Cos(lat * Math.PI / 180.0)) / Math.PI) / 2.0 * (1 << zoom));
		
	return p;
}

public PointF TileToWorldPos(double tile_x, double tile_y, int zoom) 
{
	PointF p = new Point();
	double n = Math.PI - ((2.0 * Math.PI * tile_y) / Math.Pow(2.0, zoom));

	p.X = (float)((tile_x / Math.Pow(2.0, zoom) * 360.0) - 180.0);
	p.Y = (float)(180.0 / Math.PI * Math.Atan(Math.Sinh(n)));

	return p;
}
XSLT

Requires math extensions from exslt.org. 

<xsl:transform
 xmlns:xsl="http://www.w3.org/1999/XSL/Transform"
 xmlns:m="http://exslt.org/math"
 extension-element-prefixes="m"
 version="1.0">

 <xsl:output method="text"/>
 <xsl:variable name="pi" select="3.14159265358979323846"/>
 
 <xsl:template name="tiley">
 	<xsl:param name="lat"/>
 	<xsl:param name="zoomfact"/>
 	<xsl:variable name="a" select="($lat * $pi) div 180.0"/>
 	<xsl:variable name="b" select="m:log(m:tan($a) + (1.0 div m:cos($a)))"/>
 	<xsl:variable name="c" select="(1.0 - ($b div $pi)) div 2.0"/>
	<xsl:value-of select="floor($c * $zoomfact)"/>
 </xsl:template>
 
 <xsl:template name="tilename">
 	<xsl:param name="lat"/>
 	<xsl:param name="lon"/>
 	<xsl:param name="zoom" select="10"/>
 	<xsl:variable name="zoomfact" select="m:power(2,$zoom)"/>
 	<xsl:variable name="x" select="floor((360.0 + ($lon * 2)) * $zoomfact div 720.0)"/>
 	<xsl:variable name="y">
 		<xsl:call-template name="tiley">
 			<xsl:with-param name="lat" select="$lat"/>
 			<xsl:with-param name="zoomfact" select="$zoomfact"/>
 		</xsl:call-template>
 	</xsl:variable>
 	<xsl:value-of select="concat($zoom,'/',$x,'/',$y)"/>
 </xsl:template>
 
 <xsl:template match="/">
 	<xsl:call-template name="tilename">
 		<xsl:with-param name="lat" select="49.867731999999997"/>
 		<xsl:with-param name="lon" select="8.6295369999999991"/>
 		<xsl:with-param name="zoom" select="14"/>
 	</xsl:call-template>
 </xsl:template>
</xsl:transform>
Haskell
-- https://github.com/apeyroux/HSlippyMap

long2tilex lon z = floor((lon + 180.0) / 360.0 * (2.0 ** z))

lat2tiley lat z = floor((1.0 - log( tan(lat * pi/180.0) + 1.0 / cos(lat * pi/180.0)) / pi) / 2.0 * (2.0 ** z))

tilex2long x z = x / (2.0 ** z) * 360.0 - 180

tiley2lat y z = 180.0 / pi * atan(0.5 * (exp(n) - exp(-n)))
        where
                n = pi - 2.0 * pi * y / (2.0 ** z)

-- Example
main = do
        --print $ long2tilex 2.2712 17
        --print $ lat2tiley 48.8152 17
        --print $ tilex2long 66362 17
        --print $ tiley2lat 45115 17
        putStrLn "gps: (lat=48.8152,long=2.2712)"
        putStrLn $ "https://tile.openstreetmap.org/17/" ++ show x ++ "/" ++ show y ++ ".png"
        where
                z = 17
                x = long2tilex 2.2712 z
                y = lat2tiley 48.8152 z
Scala
import scala.math._

case class Tile(x: Int,y: Int, z: Short){
  def toLatLon = new LatLonPoint(
    toDegrees(atan(sinh(Pi * (1.0 - 2.0 * y.toDouble / (1<<z))))), 
    x.toDouble / (1<<z) * 360.0 - 180.0,
    z)
  def toURI = new java.net.URI("https://tile.openstreetmap.org/"+z+"/"+x+"/"+y+".png")
}

case class LatLonPoint(lat: Double, lon: Double, z: Short){
  def toTile = new Tile(
    ((lon + 180.0) / 360.0 * (1<<z)).toInt,
    ((1 - log(tan(toRadians(lat)) + 1 / cos(toRadians(lat))) / Pi) / 2.0 * (1<<z)).toInt, 
    z)
}

//Usage:
val point = LatLonPoint(51.51202,0.02435,17)
val tile = point.toTile
// ==> Tile(65544,43582,17)
val uri = tile.toURI
// ==> https://tile.openstreetmap.org/17/65544/43582.png
Revolution/Transcript

function osmTileRef iLat, iLong, iZoom --> part path
   local n, xTile, yTile
   put (2 ^ iZoom) into n
   put (iLong + 180) / 360 * n into xTile
   multiply iLat by (pi / 180) -- convert to radians
   put ((1 - ln(tan(iLat) + 1 / cos(iLat)) / pi) / 2) * n into yTile
   return "/" & iZoom & "/" & trunc(xTile) & "/" & trunc(yTile)
end osmTileRef

function osmTileCoords xTile, yTile, iZoom --> coordinates
   local twoPzoom, iLong, iLat, n
   put (2 ^ iZoom) into twoPzoom
   put xTile / twoPzoom * 360 - 180 into iLong
   put pi - 2 * pi * yTile / twoPzoom into n
   put "n1=" && n
   put 180 / pi * atan(0.5 * (exp(n) - exp(-n))) into iLat 
   return iLat & comma & iLong
end osmTileCoords
Mathematica / Wolfram Language
Deg2Num[lat_, lon_, zoom_] := 
 {IntegerPart[(2^(-3 + zoom)*(180 + lon))/45], IntegerPart[2^(-1 + zoom)*(1 - Log[Sec[Degree*lat] + Tan[Degree*lat]]/Pi)]}

Num2Deg[xtile_,ytile_,zoom_] := 
 {ArcTan[Sinh[Pi*(1 - 2*(ytile/2^zoom))]]/Degree, (xtile/2^zoom)*360 - 180} // N
Tcl

First of all, you need to use the package map::slippy from Tcllib: 

package require map::slippy

Lat./lon. to tile number 

map::slippy geo 2tile [list $zoom $lat $lon]

Tile number to lat/lon 

map::slippy tile 2geo [list $zoom $row $col]
Pascal

(translated from the Python code above to Pascal)

Coordinates to tile numbers 

uses {...}, Math;
{...}
var
  zoom: Integer;
  lat_rad, lat_deg, lon_deg, n: Real;
begin
  lat_rad := DegToRad(lat_deg);
  n := Power(2, zoom);
  xtile := Trunc(((lon_deg + 180) / 360) * n);
  ytile := Trunc((1 - (ln(Tan(lat_rad) + (1 /Cos(lat_rad))) / Pi)) / 2 * n);
end;

Tile numbers to coordinates 

uses {...}, Math;
{...}
var
  lat_rad, n: Real;
begin
  n := Power(2, zoom);
  lat_rad := Arctan (Sinh (Pi * (1 - 2 * ytile / n)));
  lat_deg := RadtoDeg (lat_rad);
  lon_deg := xtile / n * 360.0 - 180.0;
end;
R

Coordinates to tile numbers 

deg2num<-function(lat_deg, lon_deg, zoom){
  lat_rad <- lat_deg * pi /180
  n <- 2.0 ^ zoom
  xtile <- floor((lon_deg + 180.0) / 360.0 * n)
  ytile = floor((1.0 - log(tan(lat_rad) + (1 / cos(lat_rad))) / pi) / 2.0 * n)
  return( c(xtile, ytile))
#  return(paste(paste("https://tile.openstreetmap.org", zoom, xtile, ytile, sep="/"),".png",sep=""))
}

# Returns data frame containing detailed info for all zooms
deg2num.all<-function(lat_deg, lon_deg){
  nums <- as.data.frame(matrix(ncol=6,nrow=21))
  colnames(nums) <- c('zoom', 'x', 'y', 'mapquest_osm', 'mapquest_aerial', 'osm')
  rownames(nums) <- 0:20
  for (zoom in 0:20) {
    num <- deg2num(lat_deg, lon_deg, zoom)
    nums[1+zoom,'zoom'] <- zoom
    nums[1+zoom,'x'] <- num[1]
    nums[1+zoom,'y'] <- num[2]
    nums[1+zoom,'mapquest_osm'] <- paste('http://otile1.mqcdn.com/tiles/1.0.0/map/', zoom, '/', num[1], '/', num[2], '.jpg', sep='')
    nums[1+zoom,'mapquest_aerial'] <- paste('http://otile1.mqcdn.com/tiles/1.0.0/sat/', zoom, '/', num[1], '/', num[2], '.jpg', sep='')
    nums[1+zoom,'osm'] <- paste('https://tile.openstreetmap.org/', zoom, '/', num[1], '/', num[2], '.png', sep='')
  }
  return(nums)
}
Awk (Bourne shell)

Tile numbers to lat./lon. / Coordinates to tile numbers / Sample of usage, with optional tms-format support 

xtile2long()
{
 xtile=$1
 zoom=$2
 echo "${xtile} ${zoom}" | awk '{printf("%.9f", $1 / 2.0^$2 * 360.0 - 180)}'
} 

long2xtile()  
{ 
 long=$1
 zoom=$2
 echo "${long} ${zoom}" | awk '{ xtile = ($1 + 180.0) / 360 * 2.0^$2; 
  xtile+=xtile<0?-0.5:0.5;
  printf("%d", xtile ) }'
}

ytile2lat()
{
 ytile=$1;
 zoom=$2;
 tms=$3;
 if [ ! -z "${tms}" ]
 then
 #  from tms_numbering into osm_numbering
  ytile=`echo "${ytile}" ${zoom} | awk '{printf("%d\n",((2.0^$2)-1)-$1)}'`;
 fi
 lat=`echo "${ytile} ${zoom}" | awk -v PI=3.14159265358979323846 '{ 
       num_tiles = PI - 2.0 * PI * $1 / 2.0^$2;
       printf("%.9f", 180.0 / PI * atan2(0.5 * (exp(num_tiles) - exp(-num_tiles)),1)); }'`;
 echo "${lat}";
}

lat2ytile() 
{ 
 lat=$1;
 zoom=$2;
 tms=$3;
 ytile=`echo "${lat} ${zoom}" | awk -v PI=3.14159265358979323846 '{ 
   tan_x=sin($1 * PI / 180.0)/cos($1 * PI / 180.0);
   ytile = (1 - log(tan_x + 1/cos($1 * PI/ 180))/PI)/2 * 2.0^$2; 
   ytile+=ytile<0?-0.5:0.5;
   printf("%d", ytile ) }'`;
 if [ ! -z "${tms}" ]
 then
  #  from oms_numbering into tms_numbering
  ytile=`echo "${ytile}" ${zoom} | awk '{printf("%d\n",((2.0^$2)-1)-$1)}'`;
 fi
 echo "${ytile}";
}
# ------------------------------------
# Sample of use: 
# Position Brandenburg Gate, Berlin
# ------------------------------------
LONG=13.37771496361961;
LAT=52.51628011262304;
ZOOM=17;
TILE_X=70406;
TILE_Y=42987; 
TILE_Y_TMS=88084;
TMS=""; # when NOT empty: tms format assumed
# ------------------------------------
# assume input/output of y is in oms-format:
LONG=$( xtile2long ${TILE_X} ${ZOOM} );
LAT=$( ytile2lat ${TILE_Y} ${ZOOM} ${TMS} );
# Result should be longitude[13.375854492] latitude[52.517892228]
TILE_X=$( long2xtile ${LONG} ${ZOOM} );
TILE_Y=$( lat2ytile ${LAT} ${ZOOM} ${TMS} );
# Result should be x[70406] y_oms[42987] 
# ------------------------------------
# assume input/output of y is in tms-format:
TMS="tms";
TILE_Y_TMS=$( lat2ytile ${LAT} ${ZOOM} ${TMS} );
LAT_TMS=$( ytile2lat ${TILE_Y_TMS} ${ZOOM} ${TMS} );
echo "Result should be y_oms[${TILE_Y}] latitude[${LAT}] ; y_tms[${TILE_Y_TMS}] latitude_tms[${LAT_TMS}] "
# latitude and latitude_tms should have the same value ; y_oms and y_tms should have the given start values:
# Result should be y_oms[42987] latitude[52.517892228] ; y_tms[88084] latitude_tms[52.517892228]
# ------------------------------------

Tile bounding box and center 

n=$(ytile2lat `expr ${TILE_Y}` ${ZOOM})
s=$(ytile2lat `expr ${TILE_Y} + 1` ${ZOOM})
e=$(xtile2long `expr ${TILE_X} + 1` ${ZOOM})
w=$(xtile2long `expr ${TILE_X}` ${ZOOM})

echo "bbox=$w,$s,$e,$n" 
echo "-I-> Result should be [bbox=13.375854492,52.516220864,13.378601074,52.517892228]";

center_lat=`echo "$s $n" | awk '{printf("%.8f", ($1 + $2) / 2.0)}'`
center_lon=`echo "$w $e" | awk '{printf("%.8f", ($1 + $2) / 2.0)}'`

echo "center=$center_lat,$center_lon"
echo "-I-> Result should be [center=52.51705655,13.37722778]";
Octave

Lon./lat. to tile numbers 

% convert the degrees to radians
rho = pi/180;
lon_rad = lon_deg * rho;
lat_rad = lat_deg * rho;

n = 2 ^ zoom
xtile = n * ((lon_deg + 180) / 360)
ytile = n * (1 - (log(tan(lat_rad) + sec(lat_rad)) / pi)) / 2

Tile numbers to lon./lat. 

n=2^zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = arctan(sinh(pi * (1 - 2 * ytile / n)))
lat_deg = lat_rad * 180.0 / pi
Emacs-lisp
(defun longitude2tile (lon zoom) (* (expt 2 zoom) (/ (+ lon 180) 360)))

(defun tile2longitude (x zoom) (- (/ (* x 360) (expt 2 zoom)) 180))

(defun latitude2tile (lat zoom) (* (expt 2 zoom) (/ (- 1 (/ (log (+ (tan (/ (* lat pi) 180)) (/ 1 (cos (/ (* lat pi) 180))))) pi)) 2)))
 
(defun sinh (value) (/ (- (exp value) (exp (- value))) 2))
(defun tile2latitude (y zoom) (/ (* 180 (atan (sinh (* pi (- 1 (* 2 (/ y (expt 2 zoom)))))))) pi))
Erlang
-module(slippymap).
-export([deg2num/3]).
-export([num2deg/3]).

deg2num(Lat,Lon,Zoom)->
    X=math:pow(2, Zoom) * ((Lon + 180) / 360),
    Sec=1/math:cos(deg2rad(Lat)),
    R = math:log(math:tan(deg2rad(Lat)) + Sec)/math:pi(),
    Y=math:pow(2, Zoom) * (1 - R) / 2,
    {round(X),round(Y)}.

num2deg(X,Y,Zoom)->
    N=math:pow(2, Zoom),
    Lon=X/N*360-180,
    Lat_rad=math:atan(math:sinh(math:pi()*(1-2*Y/N))),
    Lat=Lat_rad*180/math:pi(),
    {Lon,Lat}.

deg2rad(C)->
    C*math:pi()/180.
Lua
function deg2num(lon, lat, zoom)
    local n = 2 ^ zoom
    local lon_deg = tonumber(lon)
    local lat_rad = math.rad(lat)
    local xtile = math.floor(n * ((lon_deg + 180) / 360))
    local ytile = math.floor(n * (1 - (math.log(math.tan(lat_rad) + (1 / math.cos(lat_rad))) / math.pi)) / 2)
    return xtile, ytile
end

function num2deg(x, y, z)
    local n = 2 ^ z
    local lon_deg = x / n * 360.0 - 180.0
    local lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * y / n)))
    local lat_deg = lat_rad * 180.0 / math.pi
    return lon_deg, lat_deg
end
PostgreSQL
CREATE OR REPLACE FUNCTION lon2tile(lon DOUBLE PRECISION, zoom INTEGER)
  RETURNS INTEGER AS
$BODY$
    SELECT FLOOR( (lon + 180) / 360 * (1 << zoom) )::INTEGER;
$BODY$
  LANGUAGE SQL COST 1 IMMUTABLE STRICT PARALLEL SAFE;

CREATE OR REPLACE FUNCTION lat2tile(lat DOUBLE PRECISION, zoom INTEGER)
  RETURNS INTEGER AS
$BODY$
    SELECT floor( (1.0 - ln(tan(radians(lat)) + 1.0 / cos(radians(lat))) / pi()) / 2.0 * (1 << zoom) )::INTEGER;
$BODY$
  LANGUAGE SQL COST 1 IMMUTABLE STRICT PARALLEL SAFE;

CREATE OR REPLACE FUNCTION tile2lat(y INTEGER, zoom INTEGER)
  RETURNS double precision AS
$BODY$
DECLARE
 n float;
 sinh float;
 E float = 2.7182818284;
BEGIN
    n = pi() - (2.0 * pi() * y) / power(2.0, zoom);
    sinh = (1 - power(E, -2*n)) / (2 * power(E, -n));
    return degrees(atan(sinh));
END;
$BODY$
  LANGUAGE plpgsql IMMUTABLE;


CREATE OR REPLACE FUNCTION tile2lon(x integer, zoom integer)
  RETURNS double precision AS
$BODY$
 SELECT CAST(x * 1.0 / (1 << zoom) * 360.0 - 180.0 AS double precision);
$BODY$
  LANGUAGE sql IMMUTABLE;
Objective-C
+(NSString*) transformWorldCoordinateToTilePathForZoom:(int)zoom fromLon:(double) lon  fromLat:(double) lat
{
    int tileX = (int)(floor((lon + 180.0) / 360.0 * pow(2.0, zoom)));
    int tileY = (int)(floor((1.0 - log( tan(lat * M_PI/180.0) + 1.0 / cos(lat * M_PI/180.0)) / M_PI) / 2.0 * pow(2.0, zoom)));
    NSString * path = [NSString stringWithFormat:@"%d/%d/%d",zoom,tileX,tileY];
    return path;
}
Swift
func tranformCoordinate(_ latitude: Double, _ longitude: Double, withZoom zoom: Int) -> (x: Int, y: Int) {
    let tileX = Int(floor((longitude + 180) / 360.0 * pow(2.0, Double(zoom))))
    let tileY = Int(floor((1 - log( tan( latitude * Double.pi / 180.0 ) + 1 / cos( latitude * Double.pi / 180.0 )) / Double.pi ) / 2 * pow(2.0, Double(zoom))))
    
    return (tileX, tileY)
}

    func tileToLatLon(tileX : Int, tileY : Int, mapZoom: Int) -> (lat_deg : Double, lon_deg : Double) {
        let n : Double = pow(2.0, Double(mapZoom))
        let lon = (Double(tileX) / n) * 360.0 - 180.0
        let lat = atan( sinh (.pi - (Double(tileY) / n) * 2 * Double.pi)) * (180.0 / .pi)
        
        return (lat, lon)
    }
Clojure
(defn tile [lat lon zoom]
  (let [zoom-shifted (bit-shift-left 1 zoom)
        lat-radians (Math/toRadians lat)
        xtile (int (Math/floor (* (/ (+ 180 lon) 360) zoom-shifted)))
        ytile (int (Math/floor (* (/ (- 1
                                        (/
                                          (Math/log (+ (Math/tan lat-radians)
                                                       (/ 1 (Math/cos lat-radians))))
                                          Math/PI))
                                     2)
                                  zoom-shifted)))]
    (str zoom
         "/"
         (cond (< xtile 0) 0
               (>= xtile zoom-shifted) (- zoom-shifted 1)
               :else xtile)
         "/"
         (cond (< ytile 0) 0
               (>= ytile zoom-shifted) (- zoom-shifted 1)
               :else ytile))))
Julia
lng2tile(lng, zoom) = floor((lng+180)/360*2^zoom)
lat2tile(lat, zoom) = floor((1-log(tan(lat*pi/180)+1/cos(lat*pi/180))/pi)/2*2^zoom)

tile2lng(x, z) = (x/2^z*360)-180
tile2lat(y, z) = 180/pi*atan(0.5*(exp(pi-2*pi*y/2^z)-exp(2*pi*y/2^z-pi)))
Rust
use std::f64::consts::PI;
fn get_tiles(lat_deg: f64, lon_deg: f64, zoom: i32) -> (i32, i32) {
    let n = (1 << zoom) as f64;

    let x_tile = (n * (lon_deg + 180.0) / 360.0) as i32;

    let lat_rad = lat_deg.to_radians();
    let y_tile = (n * (1.0 - (lat_rad.tan() + (1.0 / lat_rad.cos())).ln() / PI) / 2.0) as i32;

    (x_tile, y_tile)
}

서브타일

타일 x,y에서 더 확대하고 싶다면, 서브타일은 (다음 확대 수준의 좌표 시스템에서) 다음과 같습니다:

2x, 2y 2x + 1, 2y
2x, 2y + 1 2x + 1, 2y + 1

마찬가지로, x와 y를 절반으로 줄이면 (이전 확대 수준에서) 축소할 수 있습니다.

해상도와 축척

적도(위키백과에 따르면)의 정확한 길이는 WGS-84 기준으로 40075.016686 km입니다. 확대 수준 0에서 한 픽셀은 156543.03 미터에 해당합니다 (타일 크기가 256 픽셀이라고 가정): 

40075.016686 * 1000 / 256 ≈ 6378137.0 * 2 * pi / 256 ≈ 156543.03

이는 임의의 확대 수준에서 해상도를 계산하는 공식을 제공합니다: 

resolution = 156543.03 meters/pixel * cos(latitude) / (2 ^ zoomlevel)

일부 애플리케이션은 화면에서 1 cm가 지도의 1 cm에 해당하는 비율을 알아야 합니다. 

scale = 1 : (screen_dpi * 1/0.0254 in/m * resolution)

다음 표는 이러한 계산을 피할 수 있도록 도와줍니다. 모든 값은 적도 기준으로 표시되며, 주어진 위도에 맞추기 위해 cos(latitude)를 곱해야 합니다. 예를 들어, 위도 60 (오슬로, 헬싱키, 상트페테르부르크)의 경우 값을 2로 나누어 조정합니다.

확대 수준 해상도, m/px 축척 90 dpi 화면 1 cm당 축척 축척 96 dpi 축척 120 dpi
0 156543.03 1 : 554 680 041 5547 km 1 : 591 658 711 1 : 739 573 389
1 78271.52 1 : 277 340 021 2773 km 1 : 295 829 355 1 : 369 786 694
2 39135.76 1 : 138 670 010 1387 km 1 : 147 914 678 1 : 184 893 347
3 19567.88 1 : 69 335 005 693 km 1 : 73 957 339 1 : 92 446 674
4 9783.94 1 : 34 667 503 347 km 1 : 36 978 669 1 : 46 223 337
5 4891.97 1 : 17 333 751 173 km 1 : 18 489 335 1 : 23 111 668
6 2445.98 1 : 8 666 876 86.7 km 1 : 9 244 667 1 : 11 555 834
7 1222.99 1 : 4 333 438 43.3 km 1 : 4 622 334 1 : 5 777 917
8 611.50 1 : 2 166 719 21.7 km 1 : 2 311 167 1 : 2 888 959
9 305.75 1 : 1 083 359 10.8 km 1 : 1 155 583 1 : 1 444 479
10 152.87 1 : 541 680 5.4 km 1 : 577 792 1 : 722 240
11 76.437 1 : 270 840 2.7 km 1 : 288 896 1 : 361 120
12 38.219 1 : 135 420 1.35 km 1 : 144 448 1 : 180 560
13 19.109 1 : 67 710 677 m 1 : 72 224 1 : 90 280
14 9.5546 1 : 33 855 339 m 1 : 36 112 1 : 45 140
15 4.7773 1 : 16 927 169 m 1 : 18 056 1 : 22 570
16 2.3887 1 : 8 464 84.6 m 1 : 9 028 1 : 11 285
17 1.1943 1 : 4 232 42.3 m 1 : 4 514 1 : 5 642
18 0.5972 1 : 2 116 21.2 m 1 : 2 257 1 : 2 821

확대 레벨을 참고하세요

도구

참고 자료

(note: Slippy tiles and Google map tiles count tile 0,0 down from the top-left of the tile grid; the TMS spec specifies tiles count up from 0,0 in the lower-left!)
Retrieved from "https://wiki.openstreetmap.org/w/index.php?title=Ko:Slippy_map_tilenames&oldid=2738008"