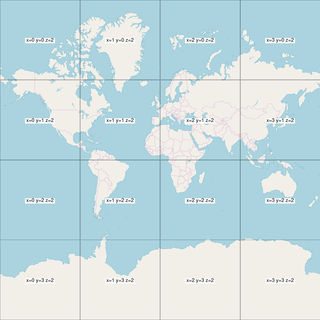
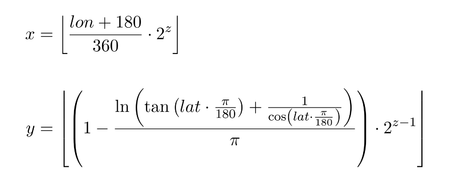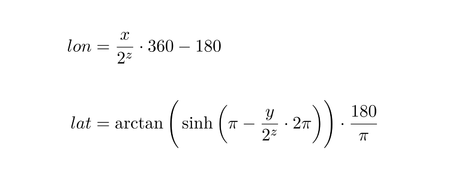Slippy map tilenames
This article describes the file naming conventions for the Slippy Map application in the OpenStreetMap website.
- Tiles are 256 × 256 pixel PNG files
- Each zoom level is a directory, each column is a subdirectory, and each tile in that column is a file
- Filename (URL) format is
/zoom/x/y.png
The slippy map expects tiles to be served up at URLs following this scheme, so all tile server URLs look pretty similar.
Tile servers
The first part of the URL specifies the tile server. The tile coordinates are typically specified by /zoom/x/y.png tail. Some tileservers will use a directory (e.g. "/cycle/") to specify a particular stylesheet. (Historically several subdomains were often provided to get around browser limitations on the number of simultaneous HTTP connections to each host - such as a.tile, b.tile, c.tile - but this is less important with modern browsers.)
Here are some examples:
| Name | URL template | zoomlevels |
|---|---|---|
| OSM 'standard' style | https://tile.openstreetmap.org/zoom/x/y.png | 0-19 |
| OpenCycleMap | http://[abc].tile.thunderforest.com/cycle/zoom/x/y.png | 0-22 |
| Thunderforest Transport | http://[abc].tile.thunderforest.com/transport/zoom/x/y.png | 0-22 |
| MapTiles API Standard | https://maptiles.p.rapidapi.com/local/osm/v1/zoom/x/y.png?rapidapi-key=YOUR-KEY | 0-19 globally |
| MapTiles API English | https://maptiles.p.rapidapi.com/en/map/v1/zoom/x/y.png?rapidapi-key=YOUR-KEY | 0-19 globally with English labels |
Further tilesets are available from various '3rd party' sources.
Zoom levels
The zoom parameter is an integer between 0 (zoomed out) and 18 (zoomed in). 18 is normally the maximum, but some tile servers might go beyond that.
| zoom level | tile coverage | number of tiles | tile size(*) in degrees |
| 0 | 1 tile covers whole world | 1 tile | 360° x 170.1022° |
| 1 | 2 × 2 tiles | 4 tiles | 180° x 85.0511° |
| 2 | 4 × 4 tiles | 16 tiles | 90° x [variable] |
| n | 2n × 2n tiles | 22n tiles | 360/2n° x [variable] |
| 12 | 4096 x 4096 tiles | 16 777 216 | 0.0879° x [variable] |
| 16 | 232 ≈ 4 295 million tiles | ||
| 17 | 17.2 billion tiles | ||
| 18 | 68.7 billion tiles | ||
| 19 | Maximum zoom for Mapnik layer | 274.9 billion tiles |
(*) While the width (longitude) in degrees is constant, given a zoom level, for all tiles, this does not happen for the height. In general, tiles belonging to the same row have equal height in degrees, but it decreases moving from the equator to the poles.
See Zoom levels for more details
Derivation of tile names
The following is identical to the well-known Web Mercator projection.
- Reproject the coordinates to the Spherical Mercator projection (from EPSG:4326 to EPSG:3857):
- x = lon
- y = arsinh(tan(lat)) = log[tan(lat) + sec(lat)]
- (lat and lon are in radians)
- Transform range of x and y to 0 – 1 and shift origin to top left corner:
- x = [1 + (x / π)] / 2
- y = [1 − (y / π)] / 2
- Calculate the number of tiles across the map, n, using 2zoom
- Multiply x and y by n. Round results down to give tilex and tiley.
Implementations
Pseudo-code
For those who like pseudo-code, here's some hints:
sec = 1/cos arsinh(x) = log(x + (x^2 + 1)^0.5) sec^2(x) = tan^2(x) + 1 → arsinh(tan(x)) = log(tan(x) + sec(x))
Please note that "log" represents the natural logarithm (also known as ln or loge), not decimal logarithm (log10), as used on some calculators.
Lon./lat. to tile numbers
n = 2 ^ zoom xtile = n * ((lon_deg + 180) / 360) ytile = n * (1 - (log(tan(lat_rad) + sec(lat_rad)) / π)) / 2
Tile numbers to lon./lat.
n = 2 ^ zoom lon_deg = xtile / n * 360.0 - 180.0 lat_rad = arctan(sinh(π * (1 - 2 * ytile / n))) lat_deg = lat_rad * 180.0 / π
This code returns the coordinate of the _upper left_ (northwest-most)-point of the tile.
Mathematics
Idem with mathematic signs (lat and lon in degrees):
Example: Convert a GPS coordinate to a pixel position in a Web Mercator tile
This example shows how to determine which tile (and what pixel coordinate within the tile) the Hachiko Statue near the Shibuya scramble crossing can be found in:
https://www.openstreetmap.org/node/597685675
1. Choose the coordinates you are interested in
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| lonEPSG:4326 | The familiar "GPS"-style longitude, which is recorded on a Node in OpenStreetMap.
Positive is east, negative is west. |
+139.7006793° |
| latEPSG:4326 | The familiar "GPS"-style latitude, which is recorded on a Node in OpenStreetMap.
Positive is north, negative is south. |
+35.6590699° |
2. Convert the coordinate to the Web Mercator projection (https://epsg.io/3857)
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| xEPSG:3857 | lonEPSG:4326
This value will fall in the range (-180°, 180°). |
139.7006793° |
| yEPSG:3857 | ln(tan(latEPSG:4326) + 1 / cos(latEPSG:4326))
OR, equivalently, arsinh(tan(latEPSG:4326)) This value will fall in the range (-π, π) for latitudes between 85.0511 °S and 85.0511 °N. For the curious, the number 85.0511 is the result of arctan(sinh(π)). By using this bound, the entire map becomes a (very large) square. |
0.66693624687 |
3. Transform the projected point onto the unit square
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| x | 0.5 + xEPSG:3857 / 360°
This value will fall in the range (0, 1). x=0 is the left (180° west) edge of the map. x=1 is the right (180° east) edge of the map. x=0.5 is the middle, the prime meridian. |
0.8880574425 |
| y | 0.5 − yEPSG:3857 / (2π)
This value will fall in the range (0, 1). y=0 is the top (north) edge of the map, at 85.0511 °N. y=1 is the bottom (south) edge of the map, at 85.0511 °S. y=0.5 is the middle, the equator. |
0.3938537996 |
4. Determine the zoom level and horizontal/vertical location of individual tiles
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| zoom | At a zoom level of 0, the entire earth is shown in a single tile.
At a zoom level of 18, detail is visible in individual city blocks. |
18 |
| N | 2zoom
This is the number of tiles horizontally or vertically from one edge of the map to the other. |
262144 |
| xtile | N * x
The whole-number part of xtile is the "x" value of the tile overall. The fractional part of xtile indicates the internal horizontal position of the coordinate within that tile. The first tile will have a xtile=0, with a left edge at 180° W. The last tile will have a xtile=2zoom−1, with a right edge at 180° E. |
232798.930207
tile x = 232798 fractional x = 93.02% |
| ytile | N * y
The whole-number part of ytile is the "y" value of the tile overall. The fractional part of ytile indicates the internal vertical position of the coordinate within that tile. The first tile will have a ytile=0, with a top edge at 85.0511 °N. The last tile will have a ytile=2zoom−1, with a bottom edge at 85.0511 °S. |
103246.410442
tile y = 103246 fractional y = 41.04% |
This results in the following tile URL:
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| URL | Most tile servers use a path similar to /(zoom)/(xtile)/(ytile).png. | https://tile.openstreetmap.org
|
5. Transform the projected point into tile space
| Variable | Formula | Example (Hachiko Statue) |
|---|---|---|
| dimension | By convention, this is 256 pixels for "standard resolution" tiles.
For "high resolution" or "retina" tiles, it's typically 512 pixels. |
256 pixels |
| xpixel | fract(xtile) * dimension
This is a number between 0 and dimension, which is the x offset of this coordinate within the tile. |
238.1 px |
| ypixel | fract(xtile) * dimension
This is a number between 0 and dimension, which is the y offset of this coordinate within the tile. |
105.1 px |
Common programming languages
Lon./lat. to tile numbers
import math
def deg2num(lat_deg, lon_deg, zoom):
lat_rad = math.radians(lat_deg)
n = 1 << zoom
xtile = int((lon_deg + 180.0) / 360.0 * n)
ytile = int((1.0 - math.asinh(math.tan(lat_rad)) / math.pi) / 2.0 * n)
return xtile, ytile
Tile numbers to lon./lat.
import math
def num2deg(xtile, ytile, zoom):
n = 1 << zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * ytile / n)))
lat_deg = math.degrees(lat_rad)
return lat_deg, lon_deg
This returns the NW-corner of the square. Use the function with xtile+1 and/or ytile+1 to get the other corners. With xtile+0.5 & ytile+0.5 it will return the center of the tile.
See also tilenames.py and the 'mercantile' library
Lon./lat. to tile numbers
def get_tile_number(lat_deg, lng_deg, zoom)
lat_rad = lat_deg/180 * Math::PI
n = 2.0 ** zoom
x = ((lng_deg + 180.0) / 360.0 * n).to_i
y = ((1.0 - Math::log(Math::tan(lat_rad) + (1 / Math::cos(lat_rad))) / Math::PI) / 2.0 * n).to_i
{:x => x, :y =>y}
end
Tile numbers to lon./lat.
def get_lat_lng_for_number(xtile, ytile, zoom)
n = 2.0 ** zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = Math::atan(Math::sinh(Math::PI * (1 - 2 * ytile / n)))
lat_deg = 180.0 * (lat_rad / Math::PI)
{:lat_deg => lat_deg, :lng_deg => lon_deg}
end
Same as the Python implementation above, this returns the NW-corner of the square. Use the function with xtile+1 and/or ytile+1 to get the other corners. With xtile+0.5 & ytile+0.5 it will return the center of the tile.
Lon./lat. to tile numbers
use Math::Trig;
sub getTileNumber {
my ($lat,$lon,$zoom) = @_;
my $xtile = int( ($lon+180)/360 * 2**$zoom ) ;
my $ytile = int( (1 - log(tan(deg2rad($lat)) + sec(deg2rad($lat)))/pi)/2 * 2**$zoom ) ;
return ($xtile, $ytile);
}
Tile numbers to lon./lat.
use Math::Trig;
sub Project {
my ($X,$Y, $Zoom) = @_;
my $Unit = 1 / (2 ** $Zoom);
my $relY1 = $Y * $Unit;
my $relY2 = $relY1 + $Unit;
# note: $LimitY = ProjectF(degrees(atan(sinh(pi)))) = log(sinh(pi)+cosh(pi)) = pi
# note: degrees(atan(sinh(pi))) = 85.051128..
#my $LimitY = ProjectF(85.0511);
# so stay simple and more accurate
my $LimitY = pi;
my $RangeY = 2 * $LimitY;
$relY1 = $LimitY - $RangeY * $relY1;
$relY2 = $LimitY - $RangeY * $relY2;
my $Lat1 = ProjectMercToLat($relY1);
my $Lat2 = ProjectMercToLat($relY2);
$Unit = 360 / (2 ** $Zoom);
my $Long1 = -180 + $X * $Unit;
return ($Lat2, $Long1, $Lat1, $Long1 + $Unit); # S,W,N,E
}
sub ProjectMercToLat($){
my $MercY = shift;
return rad2deg(atan(sinh($MercY)));
}
sub ProjectF
{
my $Lat = shift;
$Lat = deg2rad($Lat);
my $Y = log(tan($Lat) + sec($Lat));
return $Y;
}
Lon./lat. to bbox
use Math::Trig;
sub getTileNumber {
my ($lat,$lon,$zoom) = @_;
my $xtile = int( ($lon+180)/360 * 2**$zoom ) ;
my $ytile = int( (1 - log(tan(deg2rad($lat)) + sec(deg2rad($lat)))/pi)/2 * 2**$zoom ) ;
return ($xtile, $ytile);
}
sub getLonLat {
my ($xtile, $ytile, $zoom) = @_;
my $n = 2 ** $zoom;
my $lon_deg = $xtile / $n * 360.0 - 180.0;
my $lat_deg = rad2deg(atan(sinh(pi * (1 - 2 * $ytile / $n))));
return ($lon_deg, $lat_deg);
}
# convert from permalink OSM format like:
# https://www.openstreetmap.org/?lat=43.731049999999996&lon=15.79375&zoom=13&layers=M
# to OSM "Export" iframe embedded bbox format like:
# https://www.openstreetmap.org/export/embed.html?bbox=15.7444,43.708,15.8431,43.7541&layer=mapnik
sub LonLat_to_bbox {
my ($lat, $lon, $zoom) = @_;
my $width = 425; my $height = 350; # note: must modify this to match your embed map width/height in pixels
my $tile_size = 256;
my ($xtile, $ytile) = getTileNumber ($lat, $lon, $zoom);
my $xtile_s = ($xtile * $tile_size - $width/2) / $tile_size;
my $ytile_s = ($ytile * $tile_size - $height/2) / $tile_size;
my $xtile_e = ($xtile * $tile_size + $width/2) / $tile_size;
my $ytile_e = ($ytile * $tile_size + $height/2) / $tile_size;
my ($lon_s, $lat_s) = getLonLat($xtile_s, $ytile_s, $zoom);
my ($lon_e, $lat_e) = getLonLat($xtile_e, $ytile_e, $zoom);
my $bbox = "$lon_s,$lat_s,$lon_e,$lat_e";
return $bbox;
}
Lon./lat. to tile numbers
$xtile = floor((($lon + 180) / 360) * pow(2, $zoom));
$ytile = floor((1 - log(tan(deg2rad($lat)) + 1 / cos(deg2rad($lat))) / pi()) /2 * pow(2, $zoom));
Tile numbers to lon./lat.
$n = pow(2, $zoom);
$lon_deg = $xtile / $n * 360.0 - 180.0;
$lat_deg = rad2deg(atan(sinh(pi() * (1 - 2 * $ytile / $n))));
Lon./lat. to tile numbers
CFScript syntax:
<cfscript>
function longitude2tile(longitude, zoom) {
return floor((longitude + 180) / 360 * (2 ^ zoom));
}
function latitude2tile(latitude, zoom) {
return floor((1 - log(tan(latitude * pi() / 180) + 1 / cos(latitude * pi() / 180)) / pi()) / 2 * (2 ^ zoom));
}
xtile = longitude2tile(longitude, zoom);
ytile = latitude2tile(latitude, zoom);
</cfscript>
CFML syntax:
<cffunction name="longitude2tile" output="no" returntype="numeric">
<cfargument name="longitude" type="numeric" required="yes" />
<cfargument name="zoom" type="numeric" required="yes" />
<cfreturn floor((arguments.longitude + 180) / 360 * (2 ^ arguments.zoom)) />
</cffunction>
<cffunction name="latitude2tile" output="no" returntype="numeric">
<cfargument name="latitude" type="numeric" required="yes" />
<cfargument name="zoom" type="numeric" required="yes" />
<cfreturn floor((1 - log(tan(arguments.latitude * pi() / 180) + 1 / cos(arguments.latitude * pi() / 180)) / pi()) / 2 * (2 ^ arguments.zoom)) />
</cffunction>
<cfset xtile = longitude2tile(longitude, zoom) />
<cfset ytile = latitude2tile(latitude, zoom) />
Tile numbers to lon./lat.
CFScript syntax:
<cfscript>
function tile2longitude(xtile, zoom) {
return (xtile / (2 ^ zoom) * 360 - 180);
}
function tile2latitude(ytile, zoom) {
var n = pi() - 2 * pi() * ytile / (2 ^ zoom);
return (180 / pi() * atn(0.5 * (exp(n) - exp(-n))));
}
longitude = tile2longitude(xtile, zoom);
latitude = tile2latitude(ytile, zoom);
</cfscript>
CFML syntax:
<cffunction name="tile2longitude" output="no" returntype="numeric">
<cfargument name="xtile" type="numeric" required="yes" />
<cfargument name="zoom" type="numeric" required="yes" />
<cfreturn (arguments.xtile / (2 ^ arguments.zoom) * 360 - 180) />
</cffunction>
<cffunction name="tile2latitude" output="no" returntype="numeric">
<cfargument name="ytile" type="numeric" required="yes" />
<cfargument name="zoom" type="numeric" required="yes" />
<cfset var n = pi() - 2 * pi() * arguments.ytile / (2 ^ arguments.zoom) />
<cfreturn (180 / pi() * atn(0.5 * (exp(n) - exp(-n)))) />
</cffunction>
<cfset longitude = tile2longitude(xtile, zoom) />
<cfset latitude = tile2latitude(ytile, zoom) />
function lon2tile(lon,zoom) { return (Math.floor((lon+180)/360*Math.pow(2,zoom))); }
function lat2tile(lat,zoom) { return (Math.floor((1-Math.log(Math.tan(lat*Math.PI/180) + 1/Math.cos(lat*Math.PI/180))/Math.PI)/2 *Math.pow(2,zoom))); }
Inverse process:
function tile2long(x,z) {
return (x/Math.pow(2,z)*360-180);
}
function tile2lat(y,z) {
var n=Math.PI-2*Math.PI*y/Math.pow(2,z);
return (180/Math.PI*Math.atan(0.5*(Math.exp(n)-Math.exp(-n))));
}
Example for calculating number of tiles within given extent and zoom-level:
var zoom = 9;
var top_tile = lat2tile(north_edge, zoom); // eg.lat2tile(34.422, 9);
var left_tile = lon2tile(west_edge, zoom);
var bottom_tile = lat2tile(south_edge, zoom);
var right_tile = lon2tile(east_edge, zoom);
var width = Math.abs(left_tile - right_tile) + 1;
var height = Math.abs(top_tile - bottom_tile) + 1;
// total tiles
var total_tiles = width * height; // -> eg. 377
Example: Tilesname WebCalc V1.0
Lon./lat. to bbox
const EARTH_CIR_METERS = 40075016.686;
const TILE_SIZE = 256
const degreesPerMeter = 360 / EARTH_CIR_METERS;
const LIMIT_Y = toDegrees(Math.atan(Math.sinh(Math.PI))) // around 85.0511...
function toRadians(degrees) {
return degrees * Math.PI / 180;
}
function toDegrees(radians) {
return (radians / Math.PI) * 180
}
function tile2long(x,z) {
return (x/Math.pow(2,z)*360-180);
}
function lonOnTile(lon, zoom) {
return ((lon + 180) / 360) * Math.pow(2, zoom)
}
function tile2lat(y,z) {
const n=Math.PI-2*Math.PI*y/Math.pow(2,z);
return (180/Math.PI*Math.atan(0.5*(Math.exp(n)-Math.exp(-n))));
}
function latOnTile(lat, zoom) {
return (
((1 -
Math.log(
Math.tan((lat * Math.PI) / 180) + 1 / Math.cos((lat * Math.PI) / 180)
) /
Math.PI) /
2) *
Math.pow(2, zoom)
)
}
function latLngToBounds(lat, lng, zoom, width, height){ // width and height must correspond to the iframe width/height
const metersPerPixelEW = EARTH_CIR_METERS / Math.pow(2, zoom + 8);
const shiftMetersEW = width/2 * metersPerPixelEW;
const shiftDegreesEW = shiftMetersEW * degreesPerMeter;
const southTile = (TILE_SIZE * latOnTile(lat, zoom) + height/2) / TILE_SIZE
const northTile = (TILE_SIZE * latOnTile(lat, zoom) - height/2) / TILE_SIZE
return {
south: Math.max(tile2lat(southTile, zoom), -LIMIT_Y),
west: lng-shiftDegreesEW,
north: Math.min(tile2lat(northTile, zoom), LIMIT_Y),
east: lng+shiftDegreesEW
}
}
// Usage Example: create the src attribute for Open Street Map:
const latitude = 47
const longitude = 12
const zoom = 16
const width = 450
const height = 350
const bb = latLngToBounds(latitude,longitude,zoom,width,height);
const src = [
"https://www.openstreetmap.org/export/embed.html?bbox=",
bb.west,
",",
bb.south,
",",
bb.east,
",",
bb.north,
"&layer=mapnik&marker=",
latitude,
",",
longitude,
].join('');
int long2tilex(double lon, int z)
{
return (int)(floor((lon + 180.0) / 360.0 * (1 << z)));
}
int lat2tiley(double lat, int z)
{
double latrad = lat * M_PI/180.0;
return (int)(floor((1.0 - asinh(tan(latrad)) / M_PI) / 2.0 * (1 << z)));
}
double tilex2long(int x, int z)
{
return x / (double)(1 << z) * 360.0 - 180;
}
double tiley2lat(int y, int z)
{
double n = M_PI - 2.0 * M_PI * y / (double)(1 << z);
return 180.0 / M_PI * atan(0.5 * (exp(n) - exp(-n)));
}
int long2tilex(double lon, int z)
{
return (int)(Math.Floor((lon + 180.0) / 360.0 * (1 << z)));
}
int lat2tiley(double lat, int z)
{
var latRad = lat / 180 * Math.PI;
return (int)Math.Floor((1 - Math.Log(Math.Tan(latRad) + 1 / Math.Cos(latRad)) / Math.PI) / 2 * (1 << z));
}
double tilex2long(int x, int z)
{
return x / (double)(1 << z) * 360.0 - 180;
}
double tiley2lat(int y, int z)
{
double n = Math.PI - 2.0 * Math.PI * y / (double)(1 << z);
return 180.0 / Math.PI * Math.Atan(0.5 * (Math.Exp(n) - Math.Exp(-n)));
}
Example(Deg2num had changed below.) : [1]
Doc : [2]
import (
"math"
)
type Tile struct {
Z int
X int
Y int
Lat float64
Long float64
}
type Conversion interface {
deg2num(t *Tile) (x int, y int)
num2deg(t *Tile) (lat float64, long float64)
}
func (*Tile) Deg2num(t *Tile) (x int, y int) {
n := math.Exp2(float64(z))
x = int(math.Floor((lon + 180.0) / 360.0 * n))
if float64(x) >= n {
x = int(n - 1)
}
y = int(math.Floor((1.0 - math.Log(math.Tan(lat*math.Pi/180.0)+1.0/math.Cos(lat*math.Pi/180.0))/math.Pi) / 2.0 * n))
return
}
func (*Tile) Num2deg(t *Tile) (lat float64, long float64) {
n := math.Pi - 2.0*math.Pi*float64(t.Y)/math.Exp2(float64(t.Z))
lat = 180.0 / math.Pi * math.Atan(0.5*(math.Exp(n)-math.Exp(-n)))
long = float64(t.X)/math.Exp2(float64(t.Z))*360.0 - 180.0
return lat, long
}
public class slippytest {
public static void main(String[] args) {
int zoom = 10;
double lat = 47.968056d;
double lon = 7.909167d;
System.out.println("https://tile.openstreetmap.org/" + getTileNumber(lat, lon, zoom) + ".png");
}
public static String getTileNumber(final double lat, final double lon, final int zoom) {
int xtile = (int)Math.floor( (lon + 180) / 360 * (1<<zoom) ) ;
int ytile = (int)Math.floor( (1 - Math.log(Math.tan(Math.toRadians(lat)) + 1 / Math.cos(Math.toRadians(lat))) / Math.PI) / 2 * (1<<zoom) ) ;
if (xtile < 0)
xtile=0;
if (xtile >= (1<<zoom))
xtile=((1<<zoom)-1);
if (ytile < 0)
ytile=0;
if (ytile >= (1<<zoom))
ytile=((1<<zoom)-1);
return("" + zoom + "/" + xtile + "/" + ytile);
}
}
Tile bounding box
class BoundingBox {
double north;
double south;
double east;
double west;
}
BoundingBox tile2boundingBox(final int x, final int y, final int zoom) {
BoundingBox bb = new BoundingBox();
bb.north = tile2lat(y, zoom);
bb.south = tile2lat(y + 1, zoom);
bb.west = tile2lon(x, zoom);
bb.east = tile2lon(x + 1, zoom);
return bb;
}
static double tile2lon(int x, int z) {
return x / Math.pow(2.0, z) * 360.0 - 180;
}
static double tile2lat(int y, int z) {
double n = Math.PI - (2.0 * Math.PI * y) / Math.pow(2.0, z);
return Math.toDegrees(Math.atan(Math.sinh(n)));
}
import kotlin.math.*
fun getXYTile(lat : Double, lon: Double, zoom : Int) : Pair<Int, Int> {
val latRad = Math.toRadians(lat)
var xtile = floor( (lon + 180) / 360 * (1 shl zoom) ).toInt()
var ytile = floor( (1.0 - asinh(tan(latRad)) / PI) / 2 * (1 shl zoom) ).toInt()
if (xtile < 0) {
xtile = 0
}
if (xtile >= (1 shl zoom)) {
xtile= (1 shl zoom) - 1
}
if (ytile < 0) {
ytile = 0
}
if (ytile >= (1 shl zoom)) {
ytile = (1 shl zoom) - 1
}
return Pair(xtile, ytile)
}
Private Function CalcTileXY(ByVal lat As Single, ByVal lon As Single, ByVal zoom As Long) As Point
CalcTileXY.X = CLng(Math.Floor((lon + 180) / 360 * 2 ^ zoom))
CalcTileXY.Y = CLng(Math.Floor((1 - Math.Log(Math.Tan(lat * Math.PI / 180) + 1 / Math.Cos(lat * Math.PI / 180)) / Math.PI) / 2 * 2 ^ zoom))
End Function
public PointF WorldToTilePos(double lon, double lat, int zoom)
{
PointF p = new Point();
p.X = (float)((lon + 180.0) / 360.0 * (1 << zoom));
p.Y = (float)((1.0 - Math.Log(Math.Tan(lat * Math.PI / 180.0) +
1.0 / Math.Cos(lat * Math.PI / 180.0)) / Math.PI) / 2.0 * (1 << zoom));
return p;
}
public PointF TileToWorldPos(double tile_x, double tile_y, int zoom)
{
PointF p = new Point();
double n = Math.PI - ((2.0 * Math.PI * tile_y) / Math.Pow(2.0, zoom));
p.X = (float)((tile_x / Math.Pow(2.0, zoom) * 360.0) - 180.0);
p.Y = (float)(180.0 / Math.PI * Math.Atan(Math.Sinh(n)));
return p;
}
Requires math extensions from exslt.org.
<xsl:transform
xmlns:xsl="http://www.w3.org/1999/XSL/Transform"
xmlns:m="http://exslt.org/math"
extension-element-prefixes="m"
version="1.0">
<xsl:output method="text"/>
<xsl:variable name="pi" select="3.14159265358979323846"/>
<xsl:template name="tiley">
<xsl:param name="lat"/>
<xsl:param name="zoomfact"/>
<xsl:variable name="a" select="($lat * $pi) div 180.0"/>
<xsl:variable name="b" select="m:log(m:tan($a) + (1.0 div m:cos($a)))"/>
<xsl:variable name="c" select="(1.0 - ($b div $pi)) div 2.0"/>
<xsl:value-of select="floor($c * $zoomfact)"/>
</xsl:template>
<xsl:template name="tilename">
<xsl:param name="lat"/>
<xsl:param name="lon"/>
<xsl:param name="zoom" select="10"/>
<xsl:variable name="zoomfact" select="m:power(2,$zoom)"/>
<xsl:variable name="x" select="floor((360.0 + ($lon * 2)) * $zoomfact div 720.0)"/>
<xsl:variable name="y">
<xsl:call-template name="tiley">
<xsl:with-param name="lat" select="$lat"/>
<xsl:with-param name="zoomfact" select="$zoomfact"/>
</xsl:call-template>
</xsl:variable>
<xsl:value-of select="concat($zoom,'/',$x,'/',$y)"/>
</xsl:template>
<xsl:template match="/">
<xsl:call-template name="tilename">
<xsl:with-param name="lat" select="49.867731999999997"/>
<xsl:with-param name="lon" select="8.6295369999999991"/>
<xsl:with-param name="zoom" select="14"/>
</xsl:call-template>
</xsl:template>
</xsl:transform>
-- https://github.com/apeyroux/HSlippyMap
long2tilex lon z = floor((lon + 180.0) / 360.0 * (2.0 ** z))
lat2tiley lat z = floor((1.0 - log( tan(lat * pi/180.0) + 1.0 / cos(lat * pi/180.0)) / pi) / 2.0 * (2.0 ** z))
tilex2long x z = x / (2.0 ** z) * 360.0 - 180
tiley2lat y z = 180.0 / pi * atan(0.5 * (exp(n) - exp(-n)))
where
n = pi - 2.0 * pi * y / (2.0 ** z)
-- Example
main = do
--print $ long2tilex 2.2712 17
--print $ lat2tiley 48.8152 17
--print $ tilex2long 66362 17
--print $ tiley2lat 45115 17
putStrLn "gps: (lat=48.8152,long=2.2712)"
putStrLn $ "https://tile.openstreetmap.org/17/" ++ show x ++ "/" ++ show y ++ ".png"
where
z = 17
x = long2tilex 2.2712 z
y = lat2tiley 48.8152 z
import scala.math._
case class Tile(x: Int,y: Int, z: Short){
def toLatLon = new LatLonPoint(
toDegrees(atan(sinh(Pi * (1.0 - 2.0 * y.toDouble / (1<<z))))),
x.toDouble / (1<<z) * 360.0 - 180.0,
z)
def toURI = new java.net.URI("https://tile.openstreetmap.org/"+z+"/"+x+"/"+y+".png")
}
case class LatLonPoint(lat: Double, lon: Double, z: Short){
def toTile = new Tile(
((lon + 180.0) / 360.0 * (1<<z)).toInt,
((1 - log(tan(toRadians(lat)) + 1 / cos(toRadians(lat))) / Pi) / 2.0 * (1<<z)).toInt,
z)
}
//Usage:
val point = LatLonPoint(51.51202,0.02435,17)
val tile = point.toTile
// ==> Tile(65544,43582,17)
val uri = tile.toURI
// ==> https://tile.openstreetmap.org/17/65544/43582.png
function osmTileRef iLat, iLong, iZoom --> part path local n, xTile, yTile put (2 ^ iZoom) into n put (iLong + 180) / 360 * n into xTile multiply iLat by (pi / 180) -- convert to radians put ((1 - ln(tan(iLat) + 1 / cos(iLat)) / pi) / 2) * n into yTile return "/" & iZoom & "/" & trunc(xTile) & "/" & trunc(yTile) end osmTileRef function osmTileCoords xTile, yTile, iZoom --> coordinates local twoPzoom, iLong, iLat, n put (2 ^ iZoom) into twoPzoom put xTile / twoPzoom * 360 - 180 into iLong put pi - 2 * pi * yTile / twoPzoom into n put "n1=" && n put 180 / pi * atan(0.5 * (exp(n) - exp(-n))) into iLat return iLat & comma & iLong end osmTileCoords
Deg2Num[lat_, lon_, zoom_] :=
{IntegerPart[(2^(-3 + zoom)*(180 + lon))/45], IntegerPart[2^(-1 + zoom)*(1 - Log[Sec[Degree*lat] + Tan[Degree*lat]]/Pi)]}
Num2Deg[xtile_,ytile_,zoom_] :=
{ArcTan[Sinh[Pi*(1 - 2*(ytile/2^zoom))]]/Degree, (xtile/2^zoom)*360 - 180} // N
First of all, you need to use the package map::slippy from Tcllib:
package require map::slippy
Lat./lon. to tile number
map::slippy geo 2tile [list $zoom $lat $lon]
Tile number to lat/lon
map::slippy tile 2geo [list $zoom $row $col]
(translated from the Python code above to Pascal)
Coordinates to tile numbers
uses {...}, Math;
{...}
var
zoom: Integer;
lat_rad, lat_deg, lon_deg, n: Real;
begin
lat_rad := DegToRad(lat_deg);
n := Power(2, zoom);
xtile := Trunc(((lon_deg + 180) / 360) * n);
ytile := Trunc((1 - (ln(Tan(lat_rad) + (1 /Cos(lat_rad))) / Pi)) / 2 * n);
end;
Tile numbers to coordinates
uses {...}, Math;
{...}
var
lat_rad, n: Real;
begin
n := Power(2, zoom);
lat_rad := Arctan (Sinh (Pi * (1 - 2 * ytile / n)));
lat_deg := RadtoDeg (lat_rad);
lon_deg := xtile / n * 360.0 - 180.0;
end;
Coordinates to tile numbers
deg2num<-function(lat_deg, lon_deg, zoom){
lat_rad <- lat_deg * pi /180
n <- 2.0 ^ zoom
xtile <- floor((lon_deg + 180.0) / 360.0 * n)
ytile = floor((1.0 - log(tan(lat_rad) + (1 / cos(lat_rad))) / pi) / 2.0 * n)
return( c(xtile, ytile))
# return(paste(paste("https://tile.openstreetmap.org", zoom, xtile, ytile, sep="/"),".png",sep=""))
}
# Returns data frame containing detailed info for all zooms
deg2num.all<-function(lat_deg, lon_deg){
nums <- as.data.frame(matrix(ncol=6,nrow=21))
colnames(nums) <- c('zoom', 'x', 'y', 'mapquest_osm', 'mapquest_aerial', 'osm')
rownames(nums) <- 0:20
for (zoom in 0:20) {
num <- deg2num(lat_deg, lon_deg, zoom)
nums[1+zoom,'zoom'] <- zoom
nums[1+zoom,'x'] <- num[1]
nums[1+zoom,'y'] <- num[2]
nums[1+zoom,'mapquest_osm'] <- paste('http://otile1.mqcdn.com/tiles/1.0.0/map/', zoom, '/', num[1], '/', num[2], '.jpg', sep='')
nums[1+zoom,'mapquest_aerial'] <- paste('http://otile1.mqcdn.com/tiles/1.0.0/sat/', zoom, '/', num[1], '/', num[2], '.jpg', sep='')
nums[1+zoom,'osm'] <- paste('https://tile.openstreetmap.org/', zoom, '/', num[1], '/', num[2], '.png', sep='')
}
return(nums)
}
Tile numbers to lat./lon. / Coordinates to tile numbers / Sample of usage, with optional tms-format support
xtile2long()
{
xtile=$1
zoom=$2
echo "${xtile} ${zoom}" | awk '{printf("%.9f", $1 / 2.0^$2 * 360.0 - 180)}'
}
long2xtile()
{
long=$1
zoom=$2
echo "${long} ${zoom}" | awk '{ xtile = ($1 + 180.0) / 360 * 2.0^$2;
xtile+=xtile<0?-0.5:0.5;
printf("%d", xtile ) }'
}
ytile2lat()
{
ytile=$1;
zoom=$2;
tms=$3;
if [ ! -z "${tms}" ]
then
# from tms_numbering into osm_numbering
ytile=`echo "${ytile}" ${zoom} | awk '{printf("%d\n",((2.0^$2)-1)-$1)}'`;
fi
lat=`echo "${ytile} ${zoom}" | awk -v PI=3.14159265358979323846 '{
num_tiles = PI - 2.0 * PI * $1 / 2.0^$2;
printf("%.9f", 180.0 / PI * atan2(0.5 * (exp(num_tiles) - exp(-num_tiles)),1)); }'`;
echo "${lat}";
}
lat2ytile()
{
lat=$1;
zoom=$2;
tms=$3;
ytile=`echo "${lat} ${zoom}" | awk -v PI=3.14159265358979323846 '{
tan_x=sin($1 * PI / 180.0)/cos($1 * PI / 180.0);
ytile = (1 - log(tan_x + 1/cos($1 * PI/ 180))/PI)/2 * 2.0^$2;
ytile+=ytile<0?-0.5:0.5;
printf("%d", ytile ) }'`;
if [ ! -z "${tms}" ]
then
# from oms_numbering into tms_numbering
ytile=`echo "${ytile}" ${zoom} | awk '{printf("%d\n",((2.0^$2)-1)-$1)}'`;
fi
echo "${ytile}";
}
# ------------------------------------
# Sample of use:
# Position Brandenburg Gate, Berlin
# ------------------------------------
LONG=13.37771496361961;
LAT=52.51628011262304;
ZOOM=17;
TILE_X=70406;
TILE_Y=42987;
TILE_Y_TMS=88084;
TMS=""; # when NOT empty: tms format assumed
# ------------------------------------
# assume input/output of y is in oms-format:
LONG=$( xtile2long ${TILE_X} ${ZOOM} );
LAT=$( ytile2lat ${TILE_Y} ${ZOOM} ${TMS} );
# Result should be longitude[13.375854492] latitude[52.517892228]
TILE_X=$( long2xtile ${LONG} ${ZOOM} );
TILE_Y=$( lat2ytile ${LAT} ${ZOOM} ${TMS} );
# Result should be x[70406] y_oms[42987]
# ------------------------------------
# assume input/output of y is in tms-format:
TMS="tms";
TILE_Y_TMS=$( lat2ytile ${LAT} ${ZOOM} ${TMS} );
LAT_TMS=$( ytile2lat ${TILE_Y_TMS} ${ZOOM} ${TMS} );
echo "Result should be y_oms[${TILE_Y}] latitude[${LAT}] ; y_tms[${TILE_Y_TMS}] latitude_tms[${LAT_TMS}] "
# latitude and latitude_tms should have the same value ; y_oms and y_tms should have the given start values:
# Result should be y_oms[42987] latitude[52.517892228] ; y_tms[88084] latitude_tms[52.517892228]
# ------------------------------------
Tile bounding box and center
n=$(ytile2lat `expr ${TILE_Y}` ${ZOOM})
s=$(ytile2lat `expr ${TILE_Y} + 1` ${ZOOM})
e=$(xtile2long `expr ${TILE_X} + 1` ${ZOOM})
w=$(xtile2long `expr ${TILE_X}` ${ZOOM})
echo "bbox=$w,$s,$e,$n"
echo "-I-> Result should be [bbox=13.375854492,52.516220864,13.378601074,52.517892228]";
center_lat=`echo "$s $n" | awk '{printf("%.8f", ($1 + $2) / 2.0)}'`
center_lon=`echo "$w $e" | awk '{printf("%.8f", ($1 + $2) / 2.0)}'`
echo "center=$center_lat,$center_lon"
echo "-I-> Result should be [center=52.51705655,13.37722778]";
Lon./lat. to tile numbers
% convert the degrees to radians
rho = pi/180;
lon_rad = lon_deg * rho;
lat_rad = lat_deg * rho;
n = 2 ^ zoom
xtile = n * ((lon_deg + 180) / 360)
ytile = n * (1 - (log(tan(lat_rad) + sec(lat_rad)) / pi)) / 2
Tile numbers to lon./lat.
n=2^zoom
lon_deg = xtile / n * 360.0 - 180.0
lat_rad = arctan(sinh(pi * (1 - 2 * ytile / n)))
lat_deg = lat_rad * 180.0 / pi
(defun longitude2tile (lon zoom) (* (expt 2 zoom) (/ (+ lon 180) 360)))
(defun tile2longitude (x zoom) (- (/ (* x 360) (expt 2 zoom)) 180))
(defun latitude2tile (lat zoom) (* (expt 2 zoom) (/ (- 1 (/ (log (+ (tan (/ (* lat pi) 180)) (/ 1 (cos (/ (* lat pi) 180))))) pi)) 2)))
(defun sinh (value) (/ (- (exp value) (exp (- value))) 2))
(defun tile2latitude (y zoom) (/ (* 180 (atan (sinh (* pi (- 1 (* 2 (/ y (expt 2 zoom)))))))) pi))
-module(slippymap).
-export([deg2num/3]).
-export([num2deg/3]).
deg2num(Lat,Lon,Zoom)->
X=math:pow(2, Zoom) * ((Lon + 180) / 360),
Sec=1/math:cos(deg2rad(Lat)),
R = math:log(math:tan(deg2rad(Lat)) + Sec)/math:pi(),
Y=math:pow(2, Zoom) * (1 - R) / 2,
{round(X),round(Y)}.
num2deg(X,Y,Zoom)->
N=math:pow(2, Zoom),
Lon=X/N*360-180,
Lat_rad=math:atan(math:sinh(math:pi()*(1-2*Y/N))),
Lat=Lat_rad*180/math:pi(),
{Lon,Lat}.
deg2rad(C)->
C*math:pi()/180.
function deg2num(lon, lat, zoom)
local n = 2 ^ zoom
local lon_deg = tonumber(lon)
local lat_rad = math.rad(lat)
local xtile = math.floor(n * ((lon_deg + 180) / 360))
local ytile = math.floor(n * (1 - (math.log(math.tan(lat_rad) + (1 / math.cos(lat_rad))) / math.pi)) / 2)
return xtile, ytile
end
function num2deg(x, y, z)
local n = 2 ^ z
local lon_deg = x / n * 360.0 - 180.0
local lat_rad = math.atan(math.sinh(math.pi * (1 - 2 * y / n)))
local lat_deg = lat_rad * 180.0 / math.pi
return lon_deg, lat_deg
end
CREATE OR REPLACE FUNCTION lon2tile(lon DOUBLE PRECISION, zoom INTEGER)
RETURNS INTEGER AS
$BODY$
SELECT FLOOR( (lon + 180) / 360 * (1 << zoom) )::INTEGER;
$BODY$
LANGUAGE SQL COST 1 IMMUTABLE STRICT PARALLEL SAFE;
CREATE OR REPLACE FUNCTION lat2tile(lat DOUBLE PRECISION, zoom INTEGER)
RETURNS INTEGER AS
$BODY$
SELECT floor( (1.0 - ln(tan(radians(lat)) + 1.0 / cos(radians(lat))) / pi()) / 2.0 * (1 << zoom) )::INTEGER;
$BODY$
LANGUAGE SQL COST 1 IMMUTABLE STRICT PARALLEL SAFE;
CREATE OR REPLACE FUNCTION tile2lat(y INTEGER, zoom INTEGER)
RETURNS double precision AS
$BODY$
DECLARE
n float;
sinh float;
E float = 2.7182818284;
BEGIN
n = pi() - (2.0 * pi() * y) / power(2.0, zoom);
sinh = (1 - power(E, -2*n)) / (2 * power(E, -n));
return degrees(atan(sinh));
END;
$BODY$
LANGUAGE plpgsql IMMUTABLE;
CREATE OR REPLACE FUNCTION tile2lon(x integer, zoom integer)
RETURNS double precision AS
$BODY$
SELECT CAST(x * 1.0 / (1 << zoom) * 360.0 - 180.0 AS double precision);
$BODY$
LANGUAGE sql IMMUTABLE;
+(NSString*) transformWorldCoordinateToTilePathForZoom:(int)zoom fromLon:(double) lon fromLat:(double) lat
{
int tileX = (int)(floor((lon + 180.0) / 360.0 * pow(2.0, zoom)));
int tileY = (int)(floor((1.0 - log( tan(lat * M_PI/180.0) + 1.0 / cos(lat * M_PI/180.0)) / M_PI) / 2.0 * pow(2.0, zoom)));
NSString * path = [NSString stringWithFormat:@"%d/%d/%d",zoom,tileX,tileY];
return path;
}
func tranformCoordinate(_ latitude: Double, _ longitude: Double, withZoom zoom: Int) -> (x: Int, y: Int) {
let tileX = Int(floor((longitude + 180) / 360.0 * pow(2.0, Double(zoom))))
let tileY = Int(floor((1 - log( tan( latitude * Double.pi / 180.0 ) + 1 / cos( latitude * Double.pi / 180.0 )) / Double.pi ) / 2 * pow(2.0, Double(zoom))))
return (tileX, tileY)
}
func tileToLatLon(tileX : Int, tileY : Int, mapZoom: Int) -> (lat_deg : Double, lon_deg : Double) {
let n : Double = pow(2.0, Double(mapZoom))
let lon = (Double(tileX) / n) * 360.0 - 180.0
let lat = atan( sinh (.pi - (Double(tileY) / n) * 2 * Double.pi)) * (180.0 / .pi)
return (lat, lon)
}
(defn tile [lat lon zoom]
(let [zoom-shifted (bit-shift-left 1 zoom)
lat-radians (Math/toRadians lat)
xtile (int (Math/floor (* (/ (+ 180 lon) 360) zoom-shifted)))
ytile (int (Math/floor (* (/ (- 1
(/
(Math/log (+ (Math/tan lat-radians)
(/ 1 (Math/cos lat-radians))))
Math/PI))
2)
zoom-shifted)))]
(str zoom
"/"
(cond (< xtile 0) 0
(>= xtile zoom-shifted) (- zoom-shifted 1)
:else xtile)
"/"
(cond (< ytile 0) 0
(>= ytile zoom-shifted) (- zoom-shifted 1)
:else ytile))))
lng2tile(lng, zoom) = floor((lng+180)/360*2^zoom)
lat2tile(lat, zoom) = floor((1-log(tan(lat*pi/180)+1/cos(lat*pi/180))/pi)/2*2^zoom)
tile2lng(x, z) = (x/2^z*360)-180
tile2lat(y, z) = 180/pi*atan(0.5*(exp(pi-2*pi*y/2^z)-exp(2*pi*y/2^z-pi)))
use std::f64::consts::PI;
fn get_tiles(lat_deg: f64, lon_deg: f64, zoom: i32) -> (i32, i32) {
let n = (1 << zoom) as f64;
let x_tile = (n * (lon_deg + 180.0) / 360.0) as i32;
let lat_rad = lat_deg.to_radians();
let y_tile = (n * (1.0 - (lat_rad.tan() + (1.0 / lat_rad.cos())).ln() / PI) / 2.0) as i32;
(x_tile, y_tile)
}
Subtiles
If you're looking at tile x,y and want to zoom in, the subtiles are (in the next zoom-level's coordinate system):
| 2x, 2y | 2x + 1, 2y |
| 2x, 2y + 1 | 2x + 1, 2y + 1 |
Similarly, zoom out by halving x and y (in the previous zoom level)
Resolution and Scale
Exact length of the equator (according to Wikipedia) is 40075.016686 km in WGS-84. At zoom 0, one pixel would equal 156543.03 meters (assuming a tile size of 256 px):
40075.016686 * 1000 / 256 ≈ 6378137.0 * 2 * pi / 256 ≈ 156543.03
Which gives us a formula to calculate resolution at any given zoom:
resolution = 156543.03 meters/pixel * cos(latitude) / (2 ^ zoomlevel)
Some applications need to know a map scale, that is, how 1 cm on a screen translates to 1 cm of a map.
scale = 1 : (screen_dpi * 1/0.0254 in/m * resolution)
And here is the table to rid you of those calculations. All values are shown for equator, and you have to multiply them by cos(latitude) to adjust to a given latitude. For example, divide those by 2 for latitude 60 (Oslo, Helsinki, Saint-Petersburg).
| zoom | resolution, m/px | scale 90 dpi | 1 screen cm is | scale 96 dpi | scale 120 dpi |
|---|---|---|---|---|---|
| 0 | 156543.03 | 1 : 554 680 041 | 5547 km | 1 : 591 658 711 | 1 : 739 573 389 |
| 1 | 78271.52 | 1 : 277 340 021 | 2773 km | 1 : 295 829 355 | 1 : 369 786 694 |
| 2 | 39135.76 | 1 : 138 670 010 | 1387 km | 1 : 147 914 678 | 1 : 184 893 347 |
| 3 | 19567.88 | 1 : 69 335 005 | 693 km | 1 : 73 957 339 | 1 : 92 446 674 |
| 4 | 9783.94 | 1 : 34 667 503 | 347 km | 1 : 36 978 669 | 1 : 46 223 337 |
| 5 | 4891.97 | 1 : 17 333 751 | 173 km | 1 : 18 489 335 | 1 : 23 111 668 |
| 6 | 2445.98 | 1 : 8 666 876 | 86.7 km | 1 : 9 244 667 | 1 : 11 555 834 |
| 7 | 1222.99 | 1 : 4 333 438 | 43.3 km | 1 : 4 622 334 | 1 : 5 777 917 |
| 8 | 611.50 | 1 : 2 166 719 | 21.7 km | 1 : 2 311 167 | 1 : 2 888 959 |
| 9 | 305.75 | 1 : 1 083 359 | 10.8 km | 1 : 1 155 583 | 1 : 1 444 479 |
| 10 | 152.87 | 1 : 541 680 | 5.4 km | 1 : 577 792 | 1 : 722 240 |
| 11 | 76.437 | 1 : 270 840 | 2.7 km | 1 : 288 896 | 1 : 361 120 |
| 12 | 38.219 | 1 : 135 420 | 1.35 km | 1 : 144 448 | 1 : 180 560 |
| 13 | 19.109 | 1 : 67 710 | 677 m | 1 : 72 224 | 1 : 90 280 |
| 14 | 9.5546 | 1 : 33 855 | 339 m | 1 : 36 112 | 1 : 45 140 |
| 15 | 4.7773 | 1 : 16 927 | 169 m | 1 : 18 056 | 1 : 22 570 |
| 16 | 2.3887 | 1 : 8 464 | 84.6 m | 1 : 9 028 | 1 : 11 285 |
| 17 | 1.1943 | 1 : 4 232 | 42.3 m | 1 : 4 514 | 1 : 5 642 |
| 18 | 0.5972 | 1 : 2 116 | 21.2 m | 1 : 2 257 | 1 : 2 821 |
See also Zoom levels
Tools
- Geo-OSM-Tiles: a Perl module that calculates tile numbers along with a script that downloads map tiles
- Kachelbrowser
- File:Lat lon.odt feuille de calcul openoffice (sheet)
- Geofabrik map showing tile grid and coordinates on the map
- What the Quad - Get the z/x/y tile coordinate for any place on the map by just clicking on it. Also provides Bing Quadkey and lon/lat coordinates.
References
- http://cfis.savagexi.com/articles/2006/05/03/google-maps-deconstructed
- Setting up TMS
- TMS specification from the OSGeo Foundation
- (note: Slippy tiles and Google map tiles count tile 0,0 down from the top-left of the tile grid; the TMS spec specifies tiles count up from 0,0 in the lower-left!)